THE HUBBLE LAW

Introduction

Objective

To derive a value for the Hubble constant and the age of the universe.

Introduction and Overview

In the 1920's, Edwin P. Hubble discovered that distant galaxies were all moving away from the Milky Way (and th Local Group). Not only that, the farther away he observed, the faster the galaxies were receeding. He found the relationship that is now known as Hubble's Law: the recessional velocity of a galaxy is proportional to its distance from us. The equation looks like this:

v = Ho * d,

where v is the galaxy's velocity (in km/sec), d is the distance to the galaxy (in megaparsecs; 1 Mpc = 1 million parsecs), and Ho is the proportionality constant, called "The Hubble constant." This equation is telling us that a galaxy moving away from us twice as fast as another galaxy will be twice as far away, a galaxy moving away from us three times as fast will be three times farther away, and so on.

The value for the Hubble constant, which gives the age of the Universe, has been an area of ongoing debate. Even the most recent observations using the Hubble space telescope have not silenced the feuding sides. Before the HST observations, one group insisted the Hubble constant was about 100 km/sec/Mpc (giving an age for the Universe of around 10 billion years) while the other group claimed a value of 50 km/sec/Mpc (20 billion years). Although the sides moved a bit closer with additional observations, 80 km/sec/Mpc versus 60 km/sec/Mpc (12 billion years versus 17 billion years), both groups insisted that their value for the Hubble constant was, in fact, the correct value. The question for the value of the Hubble constant and the age of the Universe may, however, be resolved. Recent results (February 2003) from the Wilkinson Microwave Anisotropy Probe (WMAP) indicate that the Universe is 13.7 billion years old (Hubble constant = 73 km/sec/Mpc), with just about a 1% margin of error. Astounding results indeed!

Why such a heated debate over a single number? The Hubble Constant is one of the most important numbers in cosmology because it is a measure of the age of the universe. This long-sought-after number indicates the rate at which the universe is expanding, the velocity stemming from the primordial "Big Bang." The Hubble Constant can be used to determine the intrinsic brightness and masses of stars in nearby galaxies, examine those same properties in more distant galaxies and galaxy clusters, deduce the amount of dark matter present in the Universe, obtain the scale size of faraway galaxy clusters, and serve as a test for theoretical cosmological models.

In the short time we have remaining in this quarter, we will enter this debate as we work to determine our value for the Hubble constant and get from it the age of the Universe. Read through the following summary of the steps to be taken and get an overview of what is involved. You won't need to stay up all night making the observations, but you will need to decide which galaxies to use. Once your galaxies are chosen, you will move to finding the recessional velocity for each galaxy and its distance. Your data analysis will lead to your value for the Hubble constant, the uncertainty in the value, and the age of the Universe. This lab uses much of the knowledge you have gained over the past few weeks. Ready? Let's begin.

The Steps Towards the Hubble Constant and the Age of the Universe

Step 1: Getting to Know the Galaxies

 Our first step will be to become familiar with the images and the spectra of the galaxies with which we will be working. These images and spectra are real data, and were obtained using a CCD (charge-coupled device) on a couple of large (2 - 4 meter), ground-based telescopes. You will be sketching, classifying, and describing each galaxy

Step 2: Selecting Your Galaxies

Out of the 27 images and spectra of galaxies that are available for analysis, you will need to choose 15 to analyze (including those that may have been preselected). We want to use galaxies that have similar looks and characteristics so that we can be relatively sure we are using galaxies that are all the same actual size. We do this by seeing how they look and what their spectra are like. We want spiral galaxies; we do not want elliptical galaxies. The reason why is explained below.

Step 3: Finding the velocity of each galaxy

The velocity is relatively easy for us to measure using the Doppler effect. An object in motion (in this case, being carried along by the expansion of space itself) will have its radiation (light) shifted in wavelength. For velocities much smaller than the speed of light, we can use the regular Doppler formula:

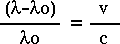The quantity on the left side of this equation is usually called the redshift, and is denoted by the letter z. The velocity of the galaxy is determined by measuring the redshift of spectral lines in the spectrum of the galaxy. The full optical spectrum of the galaxy is shown at the top of the web page containing the spectrum of the galaxy being measured. Below it are enlarged portions of the same spectrum, in the vicinity of some common galaxy spectral features: the "K and H" lines of ionized calcium and the H-alpha line of hydrogen.

Step 4: Finding the distance to each galaxy

The next step is to determine the distances to galaxies. For nearby galaxies, we can use standard candles such as Cepheid variables or white-dwarf supernovae. But, for very distant galaxies, we must rely on more indirect methods. The key assumption for this lab is that galaxies of similar Hubble type have similar actual sizes. This is known as "the standard ruler" assumption. We must first calibrate the actual size by using a galaxy to which we know the true distance. We are looking for galaxies in the sample that are spiral galaxies, as we would use nearby spiral galaxies (M31 the Andromeda galaxy, for example) to calibrate the distances. We know the distances to many nearby galaxies through observations of the Cepheid variables in them. Then, to determine the distance to very distant, but similar galaxies, one would only need to measure their apparent (angular) sizes, and use the small-angle formula.

Step 5: Data Analysis

Here is the step where you determine the Hubble constant and the uncertainty in that constant. You will be graphing the distance to each galaxy in megaparsecs (x-axis) versus the recessional velocity of that galaxy in kilometers per second (y-axis) and calculating the slope of the data -- your Hubble constant. The uncertainty in your constant is the uncertainty in the slope: what is the steepest your slope could be (highest value for the Hubble constant) and what is the shallowest (lowest value)?

With your value for the Hubble constant in hand, you are ready to calculate the age of the Universe using both a simple model for the expansion and a more realistic model that includes gravity.

Step 6: Questions

Your final step: Do you understand what you have just completed? What do some of the errors in your measurements mean? Could they have been prevented or minimized? Within your errors, do you agree with the pundits? Are you ready to challenge them?

Additional Information