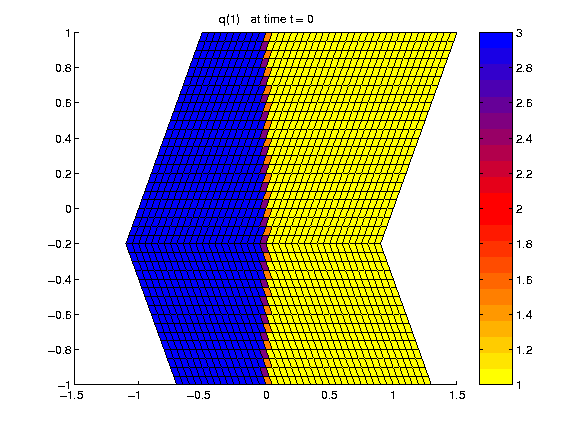
Two-dimensional Euler equations, solved on a quadrilateral grid using the mapping specified in mapc2p.f. This is currently set to cover a chevron-shaped region with a grid that is not orthogonal and not smooth along one line.
The Sod shock tube problem is solved in the x-direction.
The initial data on a coarser 40x40 version:

Density is shown, as computed on a 100 x 100 grid
Using solid wall boundary conditions at the top and bottom gives fairly good results, though with some reflection at the right boundary as the shock leaves the domain:
Using extrapolation boundary conditions at the top and bottom gives worse results with large effects also at these boundaries. This is because the extrapolation is done along grid lines rather than normal to the boundary. Better results would be obtained on a grid that is orthogonal to the boundary, or perhaps by using better extrapolation at the boundary.
For more examples of Euler on a quadrilateral grid, see claw/applications/euler/2d/quadril
Download directory in compressed tar file format (Note: Please unpack the tar file in your CLAW home directory.)