Riemann Solver Package¶
This package contains all of the Riemann solvers provided with pyclaw. Each module solves a particular type of Riemann solver listed below with but have common function signatures that look like:
rp_<name>_<dim>d(q_l,q_r,aux_l,aux_r,aux_global)
with <name> replaced with the appropriate solver name and <dim> with the appropriate dimension.
| Input: |
|
|---|---|
| Output: |
|
All of the input and output values are arrays except for aux_global which are located according to the following scheme
Indexing works like this: here mbc=2 as an example
0 1 2 3 4 mx+mbc-2 mx+mbc mx+mbc+2
| mx+mbc-1 | mx+mbc+1
| | | | | ... | | | | |
0 1 | 2 3 mx+mbc-2 |mx+mbc
mx+mbc-1 mx+mbc+1
The top indices represent the values that are located on the grid
cell boundaries such as waves, s and other Riemann problem values,
the bottom for the cell centered values. In particular the ith grid cell
boundary has the following related information:
i-1 i i+1
| | |
| i-1 | i |
| | |
Again, grid cell boundary quantities are at the top, cell centered
values are in the cell.
The arrays q_l[i], q_r are the left and right state respectively of the ith Riemann problem. All of the return values are also indexed by cell edge (Riemann problem being solved).
See [LeVeque_book_2002] for more details.
List of available Riemann solvers:
Acoustics¶
Riemann solvers for constant coefficient acoustics.
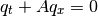
where
![q(x,t) = \left [ \begin{array}{c} p(x,t) \\ u(x,t) \end{array} \right ]](../../_images/math/41f5c43343fcd2f2372a08d6bf5edb3bd4cbdcc1.png)
and the coefficient matrix is
![A = \left [\begin{matrix}
0 & K\\
1/\rho & 0
\end{matrix} \right ]](../../_images/math/c28b6eac53d3b37c60ae8626f33dae3e89565777.png)
The parameters 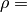 density and
density and 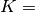 bulk modulus are used
to calculate the impedence
bulk modulus are used
to calculate the impedence 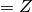 and speed of sound = c.
and speed of sound = c.
| Authors: | Kyle T. Mandli (2009-02-03): Initial version |
|---|
- pyclaw.evolve.rp.rp_acoustics.rp_acoustics_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Basic 1d acoustics riemann solver
- aux_global is expected to contain -
- zz - (float) Impedence
- cc - (float) Speed of sound
See Riemann Solver Package for more details.
Version : 1.0 (2009-02-03)
Advection¶
Simple advection Riemann solvers
Basic advection Riemann solvers of the form (1d)

| Authors: | Kyle T. Mandli (2008-2-20): Initial version |
|---|
- pyclaw.evolve.rp.rp_advection.rp_advection_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Basic 1d advection riemann solver
- aux_global should contain -
- u - (float) Determines advection speed
See Riemann Solver Package for more details.
Version : 1.0 (2008-2-20)
Burgers Equation¶
Riemann solvers for Burgers equation
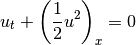
| Authors: | Kyle T. Mandli (2009-2-4): Initial version |
|---|
- pyclaw.evolve.rp.rp_burgers.rp_burgers_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Riemann solver for Burgers equation in 1d
- aux_global should contain -
- efix - (bool) Whether a entropy fix should be used, if not present, false is assumed
See Riemann Solver Package for more details.
Version : 1.0 (2009-2-4)
Euler Equations¶
Riemann solvers for the Euler equations
This module contains Riemann solvers for the Euler equations which have the form (in 1d):
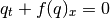
where
![q(x,t) = \left [ \begin{array}{c} \rho \\ \rho u \\ E \end{array} \right ],](../../_images/math/47146a179d9ade484afd075bfbaf33e9343ea209.png)
the flux function is
![f(q) = \left [ \begin{array}{c} \rho u \\ \rho u^2 + p \\ u(E+p) \end{array}\right ].](../../_images/math/43e7edcab595061b19841199a55fd246f799d7f3.png)
and 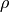 is the density,
is the density,  the velocity,
the velocity, 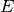 is the
energy and
is the
energy and 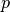 is the pressure.
is the pressure.
Unless otherwise noted, the ideal gas equation of state is used:
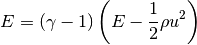
| Authors: | Kyle T. Mandli (2009-06-26): Initial version |
|---|
- pyclaw.evolve.rp.rp_euler.rp_euler_roe_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Roe Euler solver in 1d
- aug_global should contain -
- gamma - (float) Ratio of the heat capacities
- gamma1 - (float)
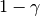
- efix - (bool) Whether to use an entropy fix or not
See Riemann Solver Package for more details.
Version : 1.0 (2009-6-26)
Shallow Water Equations¶
Riemann solvers for the shallow water equations.
- The available solvers are:
Roe - Use Roe averages to caluclate the solution to the Riemann problem
HLL - Use a HLL solver
- Exact - Use a newton iteration to calculate the exact solution to the
Riemann problem
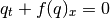
where
![q(x,t) = \left [ \begin{array}{c} h \\ h u \end{array} \right ],](../../_images/math/f235815daf1a0898b85e96783337cab945bcc3a2.png)
the flux function is
![f(q) = \left [ \begin{array}{c} h u \\ hu^2 + 1/2 g h^2 \end{array}\right ].](../../_images/math/e7f52f7633c2d6172120cced5b8910855d2ec43e.png)
and 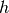 is the water column height,
is the water column height,  the velocity and
the velocity and 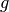 is the gravitational acceleration.
is the gravitational acceleration.
| Authors: | Kyle T. Mandli (2009-02-05): Initial version |
|---|
- pyclaw.evolve.rp.rp_shallow.rp_shallow_exact_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Exact shallow water Riemann solver
Warning
This solver has not been implemented.
- pyclaw.evolve.rp.rp_shallow.rp_shallow_hll_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
HLL shallow water solver
W_1 = Q_hat - Q_l s_1 = min(u_l-c_l,u_l+c_l,lambda_roe_1,lambda_roe_2) W_2 = Q_r - Q_hat s_2 = max(u_r-c_r,u_r+c_r,lambda_roe_1,lambda_roe_2) Q_hat = ( f(q_r) - f(q_l) - s_2 * q_r + s_1 * q_l ) / (s_1 - s_2)
- aux_global should contain:
- g - (float) Gravitational constant
Version : 1.0 (2009-02-05)
- pyclaw.evolve.rp.rp_shallow.rp_shallow_roe_1d(q_l, q_r, aux_l, aux_r, aux_global)¶
Roe shallow water solver in 1d:
ubar = (sqrt(u_l) + sqrt(u_r)) / (sqrt(h_l) + sqrt(h_r)) cbar = sqrt( 0.5 * g * (h_l + h_r)) W_1 = | 1 | s_1 = ubar - cbar | ubar - cbar | W_2 = | 1 | s_1 = ubar + cbar | ubar + cbar | a1 = 0.5 * ( - delta_hu + (ubar + cbar) * delta_h ) / cbar a2 = 0.5 * ( delta_hu - (ubar - cbar) * delta_h ) / cbar- aux_global should contain:
- g - (float) Gravitational constant
- efix - (bool) Boolean as to whether a entropy fix should be used, if not present, false is assumed
Version : 1.0 (2009-02-05)
