| Answer key to practice problems--1999 |
| 2. |
In the smaller population --
- Frequency of the recessive phenotype = (q1)2 = 4/400
- Frequency of the recessive allele = q1 = 1/10 = 0.1
In the larger population --
- Frequency of the recessive phenotype = (q2)2 = 54/600
- Frequency of the recessive allele = q2 = 1/10 = 0.3.
In the merged population --
- Frequency of recessive allele q = ((400 x 0.1) + (600 x 0.3))/1000
= 0.22
- Frequency of black cats in the next generation = q2 = (0.22)2 = 0.0484.
|
|
A potential source of error in this problem is to simply add the
number of recessive individuals from the two populations and to
derive q from that -- i.e., take the square root of (4 + 54).
However, doing so would ignore the contribution of recessive alleles
from the heterozygotes in each population. |
| 3. |
(i) |
If only black cats are left standing after the virus goes through,
then only the recessive (black) allele will be left in the population;
the frequency of the black allele in the next generation will
be 1.0 (= 100%). |
|
(ii) |
Before the virus comes through, the frequency of the three genotypes
is:
- Homozygous dominant = p2 = 0.25
- Heterozygotes = 2pq = 0.5
- Homozygous recessive = q2 = 0.25
After the viral epidemic, the only cats left are homozygous dominant
and heterozygotes:
- Homozygous dominant = p2 = 0.25
- Heterozygotes = 2pq = 0.5
Homozygous recessive = q2 = 0.25
Now the heterozygotes make up 2/3 of the surviving population,
so the recessive allele makes up 1/3 of the total alleles in the
population. Therefore, in the next generation the frequency of
black cats will be (1/3)2 = 1/9. |
| 4. |
(i) |
The d allele will be more frequent, as the forward mutation (D to d) occurs at a higher rate than the back mutation. |
|
(ii) |
Let the frequency of D = p, and the frequency of d = q, forward mutation rate = u, and back mutation rate = v
Then the change in p would include loss from forward mutation
and gain from back mutation; likewise, change in q would include
gain from forward mutation and loss from back mutation:
- Change in p = vq - up
- Change in q = up - vq
|
|
(iii) |
At equilibrium, change in p is exactly matched by change in q,
so the change in p = 0 (as is the change in q)--
- vq - up = 0;
- vq = up
- Since q = 1 - p, we can substitute and solve for p--
- v(1 - p) = up
- v - vp = up
- up + vp = v
- p = v/(u + v)
Therefore, at equilibrium, p = 0.00004/0.00016 = 0.25
- q = 1-0.25 = 0.75
|
| 5. |
(i) |
250 BB; 500 Bb |
|
(ii) |
df = 1. All we need to measure is the number of homozygous recessive
and that lets us calculate the predicted number of the other classes
(as was done in part i). |
| 6. |
(i) |
Probability of correct identification of each heterozygote = 0.7.
Therefore, the probability that both members in a heterozygote/heterozygote
couple will be correctly identified = 0.7 x 0.7 = 0.49. So the
probability that both members will not be correctly identified = 1 - 0.49 = 0.51 (or 51%). |
|
(ii) |
5% (= 0.05, the frequency of heterozygotes in the population). |
|
(iii) |
If one member is tested and not found to have a disease allele,
that could either mean that the person is homozygous normal, or
that the person is heterozygous (probability = 0.05) but is among
the 30% false negatives (probability = 0.3). So the probability
that the second person is in fact a heterozygote = 0.05 x 0.3
= 0.015. |
| 7. |
The premise of the resin treatment is that depletion of bile will
cause liver cells to express more LDL receptors so as to increase
the uptake of cholesterol. In this instance, since the cells are
incapable of expressing LDL receptors anyway, depleting the body
of bile acids will have no effect. |
| 8. |
Construct 2. The RNA transcribed from the construct has to be complementary
to the target mRNA, so it has to be transcribed off the other
strand of the template DNA (so the promoter has to be at the opposite
end of the gene, as in Construct 2). |
| 1. |
Do a complementation test... the strain with the unknown mutation
is crossed with the known torso mutant strain or the fs strain. If the unknown mutation (called mut in the diagram below) is in torso, the progeny of the cross will also have the same phenotype (tailless
offspring) -- i.e., the unknown mutation fails to complement torso and therefore the unknown mutation is in torso. Alternatively, if the unknown mutation fails to complement fs, the mutation must be in fs.

If the female progeny from Cross #1 have tailless offspring, the
unknown mutation must be in torso; if the female progeny from Cross #2 have tailless offspring,
the unknown mutation must be in fs.
There's a catch--how do we deal with the problem that the progeny
from the cross are going to be inviable? If conditional alleles (--see Answer 4 in Problem set 5) are available, there's an easy solution: do the cross and allow
development of the resulting embryos at the permissive condition,
to let the embryos develop, and then shift the young animals to
the restrictive condition to look at the phenotype of their progeny.
If conditional alleles are not available, an alternative strategy
is to cross heterozygotes and to ask if one quarter of the progeny
show the phenotype:
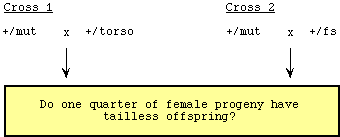
The logic here is that if mut and torso are mutations in the same gene (for example), then Cross 1 is a monohybrid cross; one quarter
of the progeny should be homozygous recessive, giving the mutant
phenotype. |
| 2. |
Transcription of Krüppel is inhibited by high levels of bicoid and hunchback. Since the level of bicoid is elevated (there will be no change in hunchback gene transcription (because increased transcription of hunchback is exactly matched by inhibition of its translation), the concentration
gradient of bicoid protein will extend further back into the embryo; the inhibition
of Krüppel gene expression will likewise extend further back, and the zone
of Krüppel gene expression will occur more to the posterior than normal.
The same result will be true of knirps also, as it too is inhibited by bicoid. |
| 3. |
The default fate of segments is to take on anterior identities;
additional genes have to be expressed to enforce posterior identities.
Therefore, expression of anterior structures in posterior regions
results from the failure to express the genes needed in the posterior
segment -- so the mutant that has wings instead of halteres shows
a recessive loss of function phenotype. In contrast, expression
of posterior structures in anterior regions must be the result
of inappropriate expression of posterior-specific genes in anterior
segments -- a dominant, gain of function phenotype. |
| 4. |
Heritability (in the broad sense) is a measure of how much of
the variability in phenotype can be ascribed to variation in genotype.
So if differences in phenotype are entirely because of differences
in genotype, heritability for that trait = 1.0. In the following
cases, if heritability is greater than 0.5, then genotype contributes
more than environment. |
|
(i) |
Genotype is more important in determining phenotype |
|
(ii) |
Genotype |
|
(iii) |
Environment is more important than genotype |
|
(iv) |
Environment |
| 5. |
(i) |
100% -- because all the environmental factors within each city are constant and uniform,
all the observed variation in IQ must be genetic. |
|
(ii) |
Any combination of genetic and environmental factors. Both the
environment and the inherited factors are different between the
two cities, so it's not possible to predict how much each factor
contributes to the variation in IQ. |
| 6. |
(i) |
40 cm (5 cm per additive allele x 4 additives, added to the base
height of 20 cm) |
|
(ii) |
- F1 will be AaBb--which has 2 additive alleles, so the height will
be 30 cm.
- F2 will be 20, 25, 30, 35, and 40 cm plants in 1:4:6:4:1 ratio.
|
|
(iii) |
- 25 cm plants have one additive allele -- genotype Aabb or aaBb.
- 35 cm plants have three additive alleles--genotype AABb or AaBB.
|
| 7. |
| gametes |
ABc (2) |
Abc (1) |
| ABC (3) |
AABBCc (5) |
AABbCc (4) |
| AbC (2) |
AABbCc (4) |
AAbbCc (3) |
| aBC (2) |
AaBBCc (4) |
AaBbCc (3) |
| abC (1) |
AaBbCc (3) |
AabbCc (2) |
The cross is AaBbCC x AABbcc. As seen from the diagram, 1/8 of
the progeny will have 2 additive alleles; the genotype of this
class will be AabbCc. (The numbers of additive alleles in parentheses.) |
| 8. |
(i) |
Quantitative inheritance. |
|
(ii) |
- The frequency of either extreme phenotype gives us n, the number of gene pairs--
- Frequency of one extreme phenotype = (1/4)n = 1/250
- # of gene pairs = log(250)/log(4) = 4.
|
|
(iii) |
The maximum contribution of additive alleles = 36 - 12 = 24 cm.
Since 8 additive alleles (4 genes) contribute 24 cm, each additive
allele contributes 3 cm. |
|
(iv) |
Each parent has 4 additive alleles; since the F1 also have 4 additive
alleles, the parents must be each be homozygous; the additive
alleles of one parent are not present in the other. For example,
the genotypes could be AABBccdd x aabbCCDD (or other genotypes
following that pattern). |
|
(v) |
- An 18 cm plant has 2 additive alleles; any genotype such as AAbbccdd
or aaBBccdd would work.
- A 33 cm plant has 7 additive alleles; any genotype such as AABBCCDd
or AaBBCCDD would work.
|
| 9. |
- There are 6 steps in height, so there can be a maximum of 6 additive
alleles--i.e., there are three gene pairs. The 10 cm plant has
only non-additive alleles; the 50 cm plant has 4 additive alleles
at two loci (i.e., it is homozygous for additive alleles at 2
loci). One example of such a cross is:
- aabbcc x AABBcc
- The F1 progeny from such a cross would be heterozygous at two
loci, and have 2 additive alleles, giving a height of 30 cm. The
F2 would be 10, 20, 30, 40, and 50 cm plants in 1:4:6:4:1 ratio
(there are 2 pairs of segregating alleles; the third locus is
homozygous, non-contributing).
|
| 10. |
500 out of 20 million individuals are homozygous dd (where D =
wildtype allele and d = disaccharide intolerance).
- If q = frequency of allele d,
- q2 = 500/20,000,000
- = 1/40,000
- q = 1/200
- Therefore, frequency of allele D = 199/200
- Frequency of heterozygotes = (2)(199/200)(1/200) = 0.0095
- The number of heterozygotes in the population = (20,000,000)(0.0095)
= 199,000.
|
| 11. |
(i) |
Let B = allele for beach-loving; b = bridge-loving
- On island 1:
- frequency of bridge-loving iguanas (genotype bb) = 0.04
- q2 = 0.04
- q = 0.2 (where q = frequency of allele b); p = frequency of allele
B = 0.8
-
- On island 2:
- frequency of bridge-loving iguanas (genotype bb) = 0.16
- q2 = 0.16
- q = 0.4; p = 0.6
-
- To look at the allele frequencies in the next generation, we can
set up a table of gamete (=allele) frequencies:
| |
p = 0.6 |
q = 0.4 |
| p = 0.8 |
0.48 |
0.32 |
| q = 0.2 |
0.12 |
0.08 |
|
So in the next generation, the frequency of bridge-loving iguanas
= q2 =0.08.
At this point, the alleles should be at Hardy-Weinberg frequencies,
so the subsequent generation will not show a change. |
|
(ii) |
This one can be solved only if we make the assumption that everyubody
gets to mate, and that all crosses produce equal numbers of progeny.
While bridge-loving iguanas are homozygous and will give rise
to bridge-loving iguanas only, beach-loving iguanas consist of
homozygotes as well as heterozygotes. So we can set up a table
as before, but this time only for frequencies of alleles B and
b within the pool of beach-loving iguanas:
- On island 1:
- p = 0.8, q = 0.2 (from part (i))
- p2 = 0.64; 2pq (homozygotes) = 0.32
- Among beach-loving iguanas, p = (0.64) + (0.32/2) = 0.8; q = (0.32/2)
= 0.16 (there's another way of getting this value too).
-
- On island 2:
- p = 0.6, q = 0.4 (from part (i))
- p2 = 0.36; 2pq (homozygotes) = 0.48
- Among beach-loving iguanas, p = (0.36) + (0.48/2) = 0.6; q = (0.48/2)
= 0.24.
| |
p = 0.6 |
q = 0.24 |
| p = 0.8 |
0.48 |
0.192 |
| q = 0.16 |
0.096 |
0.0384 |
|
Beach-loving iguanas from these crosses = (0.48)+(0.192)+(0.096)
= 0.768.
Bridge-loving iguanas = 1 - 0.768 = 0.232.
(If we didn't make the assumption stated at the beginning, we'd
just be able to make the general conclusion that homozygosity
is expected increase while heterozygosity would decrease.) |
| 12. |
Among females, the distribution of genotype frequencies is the
usual Hardy-Weinberg frequencies -- homozygous dominant = p2, heterozygotes = 2pq, homozygous recessive = q2 (where p = frequency of dominant allele, q = frequency of recessive
allele).
But in males, there are no heterozygotes for X-linked traits --
males are hemizygous for such traits. Therefore, among males,
p = frequency of the dominant phenotype; q = frequency of recessive
phenotype. |
| 13. |
(i) |
Assuming that the allele frequencies are the same in men vs. women
--
- Frequency of genotype BbBb among women = q2 = 0.09
- q = frequency of allele Bb = 0.3
- p = frequency of allele Bh = 0.7
-
- Among men, phenotypes for baldness = BbBb and BbBh.
- Frequency of genotype BbBb = 0.09
- Frequency of genotype BbBh = 2(0.3)(0.7) = 0.42
- Total frequency of bald men = 0.42 + 0.09 = 0.51; 51% of the men
become bald.
-
|
|
(ii) |
Because these are already Hardy-Weinberg frequencies, there will
be no change in allele frequencies in the next generation. |
|
1-1998
The phenotype of a (recessive) maternal effect mutation is that
females homozygous for the mutation have offspring that fail to
develop normally regardless of their genotypes. If m is the mutant allele, mm (female) x any genotype (male) should give abnormal progeny that
fail to develop correctly. In contrast, the mm genotype in males does not affect the progeny: mm (male) x M_ females will give normal, viable progeny.
[Since there is no directly observable phenotype of mm females (other than their failure to produce normal offspring),
one will have to use other markers to follow the mutagenized chromosomes.
For instance, one can mutagenize a stock that is heterozygous
for one (or more) known recessive markers on each chromosome,
mate these with non-mutagenized strains not carrying the recessive
marker alleles, and cross the F1 progeny with each other. The
F2 progeny of interest will be those displaying the recessive
marker traits--since the only source of the recessive allele is
the lone homolog (for each phenotype) that was in the mutagenized
animals, we will know that we have two copies of a chromosome
that had undergone mutagenesis--and therefore potentially homozygous
for a new mutation. In real life, one would also use balancer
chromosomes to prevent crossovers in the mutagenized chromosomes.] |
| 2-1998 |
| (i) |
The more heterozygous population is genetically more heterogeneous,
and will therefore show higher heritability than the more homozygous
population. (In the homozygous population, there is relatively
little genetic variation, so we have to ascribe a larger fraction
of the phenotypic variation to non-genetic factors. The assumption
is that both populations are showing equal amounts of phenotypic
variation.) |
| (ii) |
The population in the more uniform environment will show higher
heritability. |
| 3-1998 |
| (i) |
- Use the frequencies of the various genotype classes--
- 0.82 x 0.82 = 0.41
|
| (ii) |
|
| (iii) |
|
|
4-1998
- For the sake of simplicity, I shall designate the allele frequencies
as:
- p(Si) = a
- p(Sy) = b
- p(Sg) = c
The distribution of genotypes then is:
- (a+b+c)2 = a2 + 2ab + 2ac + b2 + 2bc + c2 = 1
- icky yucky gross
The frequencies of icky and yucky slugs are compound terms and
cannot be calculated directly. However, the frequency of gross
slugs = 0.2; c2 = 0.2, therefore c = 0.45
- But b2 + 2bc = 0.3 (= phenotype frequency of yucky slugs)
- Substituting for the value of c in this equation, we get
- b2 + 0.9b - 0.3 = 0
- Solving for b, we get b = 0.26.
-
- a = 1 - (b + c) = 0.29.
-
- p(Si) = 0.29
- p(Sy) = 0.26
- p(Sg) = 0.45
|
|
| 1. |
(a) |
The promoter is defective, so there can be no transcription of
the lac operon. |
|
(b) |
The operator is mutated, so lac repressor cannot bind -- transcription
of lac Z, Y, and A will be constitutively high regardless of whether
lactose is present or absent. However, catabolite repression is
still intact, so this constitutive transcription will occur only
when glucose is absent. |
|
(c) |
Transcription of lacZ and lacY will still be under normal inducible
control; the lacA product alone will not be made. |
|
(d) |
Depending on the nature of the missense mutation, the lacY product
(lac permease) may be functional or non-functional. Transcription
of all three lac genes should be unaffected by the mutation. [Because
the lac permease is responsible for import of lactose into the
cell, the strain may show a slower response to lactose as the
inducer than wild type.] |
|
(e) |
A stop codon near the start of the lacY coding region would likely
act as a polar mutation (the ribosome would never get to the start
codon of lacA), so the cell would produce neither lac permease
not lac transacetylase. |
|
(f) |
Without CAP, no activation of lac gene transcription can occur
regardless of whether glucose is present or absent, or whether
lactose is present or absent. |
|
(g) |
Since phosphoenol pyruvate (PEP) is one of the glycolysis products
that inhibits cAMP production (and thereby blocks CAP activation),
the failure to produce PEP will result in reduced inhibition of
CAP activation by glucose; lactose will induce lac operon transcription
even in the presence of glucose. |
| 2. |
(i) |
Constitutively high beta-galactosidase.
- i- p+ oc z+ -- the operator is defective; cannot be repressed.
- i+ p+ o+ z-
|
|
(ii) |
Constitutively low.
- i+ p+ o+ z+
- is p+ o+ z+ --the super-repressor lacIs can act in trans to repress both lacZ alleles
|
|
(iii) |
Constitutively low (no transcription of lac operon)
- i- p- oc z+ --no transcription of this lacZ allele because the promoter is
mutated
- i+ p+ oc z- --no expression of beta-gal because this lacZ allele is mutated
|
|
(iv) |
Constitutively high
- is p- o+ z+ --this lacZ is always off (no promoter, super-repressor), but
- i- p+ oc z+ the repressor can't bind to this lacOc operator; this lacZ copy is always expressed (oc is epistatic to is)
|
|
(v) |
Constitutively low (same as iii)
- i+ p- o+ z+
- i- p+ o+ z-
|
| 3. |
(a) |
gal3c will be dominant, gain-of-function: in a GAL3+/gal3c heterozygote, even if normal Gal3 protein is not binding to Gal80
(in the absence of galactose), mutant Gal3 protein can always
bind and inactivate Gal80 protein regardless of whether galactose
is present or absent. |
|
(b) |
Recessive. The mutant allele cannot provide Gal80-binding activity,
but the normal allele can -- the heterozygote can respond like
wild type. |
| 4. |
(a) |
An example of a polar mutation -- the mutation must result in
premature termination of translation such that a truncated, non-functional
protein B is made, and translation of gene C coding sequence does
not occur. |
|
(b) |
A key point to note here is that various types of mutations can
occur in any gene. A transcription activator can be mutated so
that it is incapable of activation, or it be mutated so that it
always activates, even when it's not supposed to. Likewise, a
repressor could be mutated so that it never represses or so that
it always represses.
The reg gene product must be a regulator of transcription of operon ABC.
It could either be an activator or a repressor.
Possibility 1 -- reg is an activator of transcription. An "always on" mutant phenotype
must be the result of a mutant activator that constitutively (and
inappropriately) activates transcription. The mutant phenotype
is expected to be dominant, because even if normal protein is
being made and only activates transcription when appropriate,
the mutant protein will always activate transcription. The "never
on" mutant phenotype in this scenario must the result of mutant
activator protein that fails to activate -- and this phenotype
will be recessive.
Possibility 2 -- reg is a repressor of transcription. The "always on" phenotype must
be a recessive mutation that allows transcription when appropriate;
the "never on" phenotype must be from a dominant mutation that
always represses transcription.
Looking at the actual results, we see that the the data support
possibility 1 and not possibility 2: the "always on" phenotype is dominant and the "never on" phenotype
is recessive. Therefore, reg must be an activator of ABC gene transcription. |
| 5. |
The mutation must be in a zygotic gene -- the gene product is
only needed after the first few divisions, when transcription
of that gene starts up in the developing embryo. |
| 6. |
(a) |
nanos mutations are maternal effect mutations -- females homozygous
for the mutation produce eggs that lack nanos protein. Consequently,
the posterior segments in the embryo fail to develop normally
(the posterior of the embryo is where nanos protein normally is
localized). The mutation is lethal. |
|
(b) |
This is a zygotic gene; failure to produce hunchback protein results
in los of anterior segments. This mutation is lethal also. |
| 1. |
(i) |
Because the two mutant strains showed complementation (the F1 were able to see), the mutations must have been in separate genes; the simplest explanation is that there are two genes involved.
This conclusion is supported by the F2 ratio, which can be derived
from a dihybrid ratio. |
|
(ii) |
The 9:7 F2 ratio indicates that we are dealing with a dihybrid
ratio (the fractions go in sixteenths). The 9:7 ratio can be derived
from the standard 9:3:3:1 ratio if we postulate the following
--
- Progeny that have at least one dominant allele for each gene show the dominant phenotype (normal vision) -- giving 9/16 progeny
with normal vision
- Progeny that lack a dominant allele for any gene show the recessive
phenotype (blindness) -- giving 7/16 blind progeny
If we call the two genes D and E, the parents were ddEE and DDee; the F1 progeny are DdEe (and can therefore see); the F2 progeny are:
| D_E_ |
D_ee |
ddE_ |
ddee |
- 9/16
- normal vision
|
- 3/16
- blind
|
- 3/16
- blind
|
- 1/16
- blind
|
If the F1 crickets were crossed to homozygous recessive crickets
(i.e., DdEe x ddee) the progeny would be DdEe, Ddee, ddEe, and ddee in equal proportions -- i.e., 1/4 of the progeny will be able
to see, and 3/4 will be blind. |
|
(iii) |
As with any dihybrid cross, one quarter of the progeny will be
true breeding. |
| 2. |
(i) |
As with any independently assorting pair of genes,we can look
at the the ratios for the two genes independently. With respect
to presence or absence of color (gene E), the progeny are 1/2 colored (black or brown) and half yellow.
Therefore, with respect to gene E, the parents were Ee and ee. With respect to black vs. brown (gene B), the brown parent has to be bb and the other parent must be Bb (there must be at least one B allele to give black progeny; it cannot be BB, or there would be no brown progeny). [Another way to think about this is that of the non-yellow progeny,
half are brown and half black; therefore, the parents must be
bb and Bb giving 1:1 B_ and bb progeny.]
Thus, the parents must be bbEe (brown) and Bbee (yellow). |
|
(ii) |
Here, with respect to gene E, one quarter of the progeny show the homozygous recessive phenotype--therefore
both parents must be heterozygous (Ee) for gene E. With respect to gene B, again, black and brown progeny are in equal proportions, so
the parents must be Bb and bb. Once again, the brown parent must be bbEe; the black parent must be BbEe. |
| 3. |
 This is an example of recessive epistasis. The fact that homozygous
B and homozygous O rats could generate AB progeny, and the fact that the F2 progeny fractions are in sixteenths,
tells us that this is a dihybrid cross--i.e., a second gene is
involved in addition to the IA/IB/IO (hereafter abbreviated A/B/O) gene. The A allele, which manifests itself in the F1, must have been present
in homozygous form in the O parent, but masked by the effect of the second gene, thereby
giving an O phenotype. (Why homozygous? Because if it were heterozygous, the F1 progeny
would show other phenotypes besides AB. Likewise, the A allele could not have been hiding in the B parent, because then the B parent would not be true-breeding.) Furthermore, it must be the recessive allele of the second gene (which we shall call h, the dominant allele being H) that prevents expression of the A/B allele. (Why? Because if masking allele were dominant, F1 progeny would
all express the masking phenotype, and would all be O.) The recessive h allele is epistatic to A and B. Thus, the B parent is BBHH and shows the B phenotype; the O parent is AAhh, which does not express the A allele and appears to be O. The F1 progeny are ABHh, and express both A and B alleles. One quarter of the F2 progeny are homozygous recessive
(hh); these again appear to be O because the H allele is required for expression of A and B. This is an example of recessive epistasis. The fact that homozygous
B and homozygous O rats could generate AB progeny, and the fact that the F2 progeny fractions are in sixteenths,
tells us that this is a dihybrid cross--i.e., a second gene is
involved in addition to the IA/IB/IO (hereafter abbreviated A/B/O) gene. The A allele, which manifests itself in the F1, must have been present
in homozygous form in the O parent, but masked by the effect of the second gene, thereby
giving an O phenotype. (Why homozygous? Because if it were heterozygous, the F1 progeny
would show other phenotypes besides AB. Likewise, the A allele could not have been hiding in the B parent, because then the B parent would not be true-breeding.) Furthermore, it must be the recessive allele of the second gene (which we shall call h, the dominant allele being H) that prevents expression of the A/B allele. (Why? Because if masking allele were dominant, F1 progeny would
all express the masking phenotype, and would all be O.) The recessive h allele is epistatic to A and B. Thus, the B parent is BBHH and shows the B phenotype; the O parent is AAhh, which does not express the A allele and appears to be O. The F1 progeny are ABHh, and express both A and B alleles. One quarter of the F2 progeny are homozygous recessive
(hh); these again appear to be O because the H allele is required for expression of A and B. |
|
[A note on the mechanism of blood group expression: Remember that
the A and B blood groups represent different forms of polysaccharides added
to the surface of blood cells. The molecule to which these polysaccharides
are added is the H group on the surface of red blood cells. An OO homozygote makes neither polysaccharide, and is blood type O.
But hh homozygotes, even if they are making A or B or both polysaccharides, still have an O blood type because the H moiety is not made; there is nowhere for the A or B polysaccharide to be added to. This form of O bloodtype is often called the "Bombay phenotype" because it was
discovered in a patient in Bombay, in 1952.] |
| 4. |
A selection for Ade+ revertants: plate ade- cells on agar plates lacking adenine. Only Ade+ revertants will be able to grow and form colonies. Therefore,
any yeast colonies that form on these plates must have a functional
ADE gene. |
|
A screen: grow the cells as before and plate them on medium containing
adenine. All cells (ade- and Ade+ revertants) will be able to grow, but only the Ade+ revertants will form white colonies. Examine each colony and
pick out the white ones to get the Ade+ revertants. |
| 5. |
- Remember that alleles that fail to complement each other (i.e.,
fail to give the normal phenotype) must be alleles of the same
gene. In this example, there are three complementation groups
(three genes) --
- Gene 1: p1 and r2
- Gene 2: p2, r1, and r4
- Gene 3: p3 and r3
- (Half the table is left blank because filling it would be redundant
-- p1 x r3 is the same as r3 x p1, for instance.)
|
| 6. |
(i) |
D and E will rescue (because if either one is provided, E3 function
will no longer be needed); C will accumulate (because there is
no E3 to convert C to D). |
|
(ii) |
E will rescue; D will accumulate |
|
(iii) |
D and E will rescue; B will accumulate. |
| 7. |
(i) |
Conversion of B to D cannot proceed, so D and F will each rescue
this mutation. |
|
(ii) |
Conversion of A to B cannot proceed, so B will rescue. |
| 8. |
(i) |
Red pigment cannot be made, so the flowers will be blue. |
|
(ii) |
Red flowers. |
|
(iii) |
Purple flowers (because of complementation-- the F1 will be heterozygous
for each gene). |
|
(iv) |
9/16 purple: 3/16 red: 3/16 blue: 1/16 white. |
| 9. |
Remember that a mutation in the last gene in the pathway can only
be rescued by the final product; a mutation in the next-to-last
gene can be rescued by the last two compounds in the pathway,
etc. Thus, the pathway is:

|
| 10. |
(i) |
Neither intermediate (pyrimidine or thiazole) rescues more than
one mutation. If these compounds are intermediates in a linear
pathway, we'd expect that one of them should rescue more than
one mutation. (For instance, in Q. 4, histidinol phosphate rescues
both M4 and M1 mutations.) |
|
(ii) |

(Thiazole rescues thi-1, so the problem with thi-1 must be thiazole
synthesis; likewise, the problem with thi-2 must be pyrimidine
synthesis. thi-3 is rescued only be thiamine, so it must be the
last step, the point of convergence of the two branches.) |
| 11. |

|
| 12. |
- B is required for any color, so it must be required for conversion
of white to color -- it is epistatic to A and to C.
- A appears to be required for conversion of a red intermediate to
orange -- absence of A gives a red color instead of orange.
- C is not required for pigment production, but rather, appears to
be needed to prevent pigment production in a portion of the flower,
keeping that portion white.
- B- and C- have opposite phenotypes (no color vs. too much color) so their
interaction must be negative.
Putting all this together, we can come up with at least two pathways
that can each explain the data -- one in which C regulates B directly, and one in which C acts to convert some pigmented areas back to white.

Clearly, in either model, there must be some other gene that controls
which portion of the flower are gong to express C (to make white)
and which repress C (to allow color). |
| 13. |
(i) |
CLB is required for DNA synthesis (any strain that lacks CLB function
fails to do DNA synthesis). |
|
(ii) |

SIC and CLB mutations have opposite effects, and CLB is epistatic
to SIC, so SIC must be an inhibitor of CLB. By the same logic,
CLN is an inhibitor of SIC. An alternative pathway--

-- is also possible, but the cln-sic- double mutant phenotype
argues against it. This double mutant shows too much DNA synthesis.
If CLN is required for CLB function, as this second pathway implies,
then the double mutant should show no DNA synthesis. So the data
are most consistent with the pathway at the top. |
| 1. |
(i) |
The patches probably arose by mitotic recombination. Recombination
between the two loci would give lone spots of the recessive phenotype
of the more centromere-distal locus, while recombination between
the centromere and the two loci would give twin spots. From this
logic, we can conclude that the rd locus must be closer to the centromere than the b locus. (An alternative explanation for the lone spots is mitotic
nondisjunction, but that wouldn't explain the twin spots.)

|
|
(ii) |
Because the twin spots and lone spots occurred in 6:5 ratio, the
centromere-rd distance and the rd-b distance must be in the approximate ratio of 6:5:
|
|
(iii) |
Lone spots of rd phenotype could arise either from mitotic nondisjunction or by
mitotic recombination with double crossover, one crossover between
the centromere and rd and one crossover between rd and b.

|
| 2. |
- The most distal markers must be y and g. Because yellow and rough are seen in twin spots with each other,
but not with mottled or sparse--therefore, the y and r genes must lie on one arm of the chromosome. Likewise, m and g must lie on the other arm of the chromosome. Therefore, the gene
order on the chromosome is:
- y------r-----------------------centromere-----m-------------g
- |--7---------------32----------------------6---------12
|
| 3. |
The strain described in lecture had the dominant alleles for yellow
and singed in trans. If the dominant alleles are in cis, a crossover
between the centromere and the teo genes can give a single spot
that has both recessive phenotypes:

|
| 4. |
The map is:

If a recombinant sector has phenotype a alone, then the crossover must have occurred between a and all the other genes; if a sector has phenotypes a and b, then b must be between a and all the other genes, etc. |
| 5. |
- The number of generations needed to give the final number of cells
can be deduced from the expression:
- 2n = final # of cells (where n = number of generations)
- n = log(final # of cells)/log(2)
- (e.g., if the final # of cells = 16, 2n = 16; n = 4
- For a tumor with 109 cells, n = log(109)/log(2) = 29.9 or 30 generations
|
|
The number of cell divisions = (final # of cells - 1). [Note that the number of cell divisions is not the same as the number of cell generations. In the first generation,
there is one cell dividing, so there is one division. In the second
generation, there are two cells dividing, so there are two divisions
in this generation; in the third generation, there are 4 cells
dividing, so there are 4 divisions. So after three generations,
there are 8 cells--but it took (1 division in the 1st generation)
+ (2 divisions in the 2nd generation) + (4 divisions in the 3rd
generation) = 7 divisions total.] |
| 6. |
The tumor was derived from a single cell that had one X chromosome
inactivated; since X inactivation is stably propagated through
mitosis, all daughters of that cell have the same inactive X. |
| 7. |
There must have been more than one genetic change in the history
of the tissue culture cells. For example, the cells had to go
through crisis to become immortalized, a process which probably
involved some genetic change. |
| 8. |
A mutation that results in the erbB protein behaving as though
it had bound to a growth factor even in the absence of the growth
factor could cause the cell to begin dividing in the absence of
growth factor. If other regulatory mechanisms are also abrogated
(by unrelated events), the cell or its descendants could become
malignant. |
| 9. |
(a) |
For the mutant allele (a*) to cause inappropriate cell proliferation, it must be resistant
to inhibition by Protein B. Therefore, the mutant protein made
by this allele will be able to promote cell proliferation regardless
of whether the other allele of gene A is wildtype or mutant --
so a* is a dominant, gain-of-function mutation. |
|
(b) |
Here, the mutant allele must be promoting cell proliferation by
failing to block Protein A. However, even if this allele fails
to make functional protein B, the other allele (if it is wildtype)
can still make functional Protein B and block Protein A. Therefore,
b* must be a recessive, loss-of-function mutation. |
|
(c) |
2 x 10-5 (because there are two copies of allele a+, and mutation of either one of them would be sufficient to cause
inappropriate cell proliferation). |
| 1. |
*Corrected*
There must have been two crossovers -- one between B and D and
one between F and G, as shown:

|
| 2. |
(a) |
The result is unexpected in that we are seeing only the parental
(non-crossover) products--we should see some recombinants. One
of the parents must have an inversion such that the recombination
products are inviable. |
|
(b) |
The fact that chromosomal material gets stretched between the
spindle poles and breaks suggests that a dicentric chromosome
must be formed -- indicating that the inversion must be a paracentric
inversion:
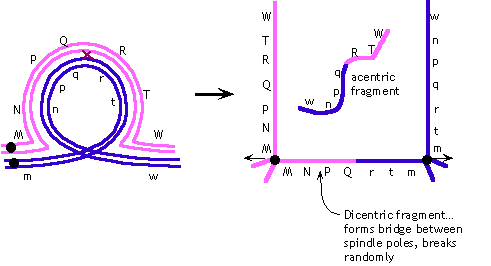
Note that the gene order shown is arbitrary; the question does
not give information on the correct gene order or even which parent
had the inversion. All we can say is that there must have been
an odd number of crossovers in the inversion loop. |
| 3. |
Deleterious effects (loss or duplication of genes leading to reduction
in fertility) will be seen when there is an odd number of crossovers
within the inversion loop. Here, the b-d-e-f segment is inverted, so that portion will form an inversion loop
during prophase of meiosis I; y-a and g-h will remain outside the loop. |
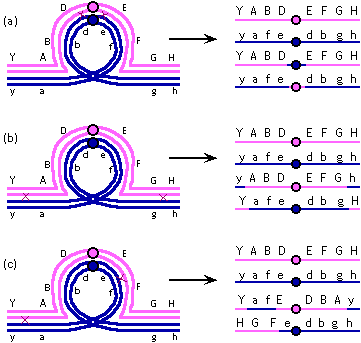 |
|
(a) |
There are two crossovers in the inversion loop, so the products
will all be viable -- no reduction in fertility. |
|
(b) |
The crossovers are both outside the inversion loop, so again,
there will be no reduction in fertility. |
|
(c) |
Here, there is only one crossover within the inversion loop, the
other crossover occurring outside the loop. This DCO event will
produce gametes with gene deletions, and will be deleterious,
leading to decreased fertility. |
| 4. |
The male progeny are expected to receive Xsc from the mother and therefore have scute bristles. This male
must have received X+ from his father (the only source of the dominant allele in the
cross). Presumably, the X-ray treatment caused a translocation
of the end of the X chromosome carrying sc+ such that the sc+ allele was transmitted to that son. |
 |
|
What about the second cross? If the translocation had been to
an autosome, the exceptional son would have had some wildtype
daughters. The fact that the wildtype phenotype segregates exclusively
with male progeny indicates that the translocation must have been
to the Y chromosome.
NOTE: Only the gametes producing the aberrant (unexpected) offspring
are shown for cross 1. Most of the gametes were normal, producing
the expected offspring.
|
| 5. |
(a) |
One way of distinguishing between the hypotheses is to obtain
DNA from affected individuals and do a Southern blot experiment
on the DNA, cutting it with EcoRI and probing the blot with the
2.5 kb fragment. As a control, this sample would be compared with
DNA from an unaffected individual. The control DNA should give
a 2.5 kb fragment on the Southern blot. If the translocation does
indeed remove the left end of the gene and replace it with an
unrelated fragment from a different chromosome, it is highly unlikely
(but not impossible) that this unrelated sequence will also have
an EcoRI site at exactly the same place -- so the DNA from the
affected person should show a fragment of a different size than
the normal 2.5 kb. (It's not possible from the available information
to make a prediction about exactly what size to expect.) In addition,
the left end, which got moved to a different chromosome, will
be part of a different EcoRI fragment in its new location. So
the affected individual, instead of producing one 2.5 kb fragment,
will probably produce two fragments of different sizes. If the
translocation does not break the growth factor gene (the minority
view), the 2.5 kb fragment should remain intact in all samples. |
|
(b) |
The same 2.5 kb probe could be used to do a FISH experiment, again
comparing cells from affected vs. unaffected individuals. In non-patients,
the probe should hybridize only to one chromosome (but to both
homologs of that chromosome) -- e.g., if the growth factor gene
is on chromosome 9, we should see hybridization to the two homologs
of chromosome 9. In patients, a portion of the growth factor gene
should be translocated to a different chromosome (according to
the prevailing hypothesis). Therefore, a FISH experiment should
detect hybridization not only to chromosome 9, but also to the
other chromosome involved in the translocation. If the minority
view is correct, only one chromosome type should be detected in
patients as well as non-patients. |
|
(c) |
The Southern blot approach only detects fragment sizes, not chromosomal
locations. As noted in (a), there is a remote possibility that
the translocation will produce exactly the same EcoRI fragment
sizes as the normal chromosome. The result would then support
the minorityview even even if the gene is indeed split by the
translocation. The FISH approach detects the chromosomal location
of the sequence being probed, and is not subject to this limitation.
Therefore, if done correctly (with a suitably large sample size
-- number of cells examined) the FISH results might be more believable.
In reality, one would probably do both tests. Technically, the
Southern blot is a lot easier. |
| 6. |
(a) |
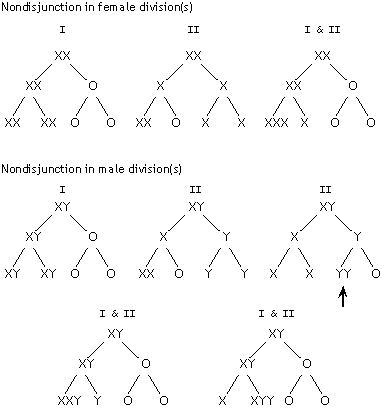 |
|
(b) |
There is just one way to get XYY progeny from normal XX and XY
parents (if nondisjunction happens only in one parent) -- male
nondisjunction in meiosis II to produce YY sperm (marked with
an arrow in the diagram). |
| 7. |
(a) |
The calico pattern is the result of X-inactivation. Male mammals
aren't expected to show X chromosome inactivation, so this result
is unexpected. The calico males are probably XXY cats, resulting
from sex chromosome nondisjunction in one of the parents. |
|
(b) |
In the first litter, the mom was XrXr and the dad was XRY. The mom could transmit only Xr; the XR allele must have come from the dad along with Y, so nondisjunction
must have occurred in the dad.
In the second litter, the mom was XRXr and the dad was XRY. The male calico kitten could have received XRXr from the mom (ND in mom) or XRY from the dad (ND in dad)-- it's not possible to distinguish
between these possibilities. |
| 8. |
(a) |
It should worse for females than for males. Deletion of XIC on
a chromosome prevents that X chromosome from being counted and
inactivated. In males, there shouldn't be X chromosome inactivation
anyway, so the deletion shouldn't matter. In female progeny, the
consequence will be that X chromosomes will be undercounted. (An
X chromosome lacking the XIC is not "seen" as an X.) Therefore,
neither X chromosome will get inactivated, which has deleterious
consequences. |
|
(b) |
The X with intact Xist will get inactivated -- Xist works in cis, so only the chromosome producing it will get inactivated. |
|
(c) |
The hypothesis is that this protein is produced in limiting quantities
so that only one X can be protected from inactivation. If the
amount of protein in the cell is doubled by the mutation, there
should be enough protein to protect both X chromosomes -- so neither
X should be inactivated. |
|
(d) |
This is an example of a dominant, "gain-of-function" mutation.
The mutated allele of this gene will produce excess protein, so
it doesn't matter if the normal allele is present also -- the
effect of the excess protein will be seen anyway. |
| 1-1998 |
| (i) |
The 38-year old has a higher risk of a Down syndrome baby, because
the probability of nondisjunction during meiosis increases with
age in human females. |
| (ii) |
The family history of Down syndrome suggests that this may be
a case of translocation Down syndrome -- in which case, the younger
woman (belonging to that family) has a higher risk of a Down syndrome
baby (because the chance of nondisjunction in a 38-year old woman
is about 1 in 100 -- see pg 69 of the lecture notes -- while the
chance of translocation Down carrier having a Down baby is 1 in
4). |
| 2-1998 |
|
| (i) |
The mother must have been heterozygous G/g, while the father was hemizygous normal G/(Y). Colorblind Turner syndrome (XO) females must have resulted from
fertilization of a g egg by a sperm lacking a sex chromosome; nondisjunction could
have occurred at meiosis I or meiosis II in the father. Colorblind
Klinefelter (XXY) males must have resulted from fertilization
of gg eggs by normal Y-bearing sperm; nondisjunction occurred in meiosis
II in the mother. |
| (ii) |
Identical (monozygotic) twins arise when an early embryo splits
so that each portion develops into an individual fetus. In this
instance, the zygote must have been normal. The split occurred
at the two-cell stage; one of the resulting cells divided normally,
giving the normal twin, while the other cell had a mitotic nondisjunction,
giving the Down syndrome twin. |
 |
| 3-1998 |
| (i) |
The F1 females should be heterozygous at all loci. We would normally
expect to see recombination in each interval, giving up to 26 = 64 different progeny phenotypes (in a ratio that would depend
on the map distances). The presence of only four progeny phenotypes
is not normally to be expected. (One could postulate that pairs
of loci are very tightly linked, but that does not explain the
lack of recombinants between the ends of the group.) |
| (ii) |
A deletion could be ruled out because half the F2 males would
inherit an X chromosome lacking genes, and would probably fail
to develop. Translocations are also unlikely to give the observed
results, because the phenotype is a reduction in observed recombinant
progeny (translocations cause semisterility, but there is no reason
not to expect recombinants (draw it out and confirm it for yourself). |
| (iii) |
The lack of recombination between A and B and between F and G
suggests that the entire portion between A and G (i.e., B through
F) is inverted. |
| (iv) |
| A variety of molecular tests is possible. For example, if the
inversion is as predicted, one can set up Southern blots, using
probes for the presumptive junction regions. In the example shown
here, Probes 1 and 2 will hybridize to different restriction fragments (of different sizes) if the chromosome is normal. In contrast,
if the inversion is as shown, probes 1 and 2 will both hybridize
to the same fragment. [Restriction enzyme sites are depicted as vertical bars. Knowing
the restriction map for the whole chromosome, we can pick a restriction
enzyme that has suitably located sites as shown.] |
 |
|
| (v) |
Single crossovers are not expected to give viable recombinant
gametes. However, rare double crossovers can be viable. In this
instance, a double crossover -- one crossover between B and D
loci and one between E and F -- would give the observed result. |
| 4-1998 |
|
If the two T-allele bearing homologs are called T1 and T2, and the two t-allele bearing homologs are t1 and t2, there are three possible sets of pairings, giving the gametes
shown:
| Pairing |
Gamete genotypes |
| T1T2 and t1t2 (i.e., T1 homolog paired to T2 homolog, etc.) |
T1t1, T2t2, T1t2, T2t1 |
| T1t1 and T2t2 |
T1T2, t1t2, T1t2, T2t1 |
| T1t2 and T2t1 |
T1T2, t1t2, T1t1, T2t2 |
The gamete genotypes are TT, Tt and tt in 1:4:1 ratio, or 5:1
ratio of T_:tt. If mated to tttt plants (whose gametes will all
be tt), the progeny are expected to be T___:tttt (i.e., tall and
short) in 5:1 ratio. |
| 5-1998 |
| (i) |
Because the plant height and color genes are on separate chromosomes,
they should assort independently; the cross should give TD, Td, tD, and td progeny in 1:1:1:1 ratio. Instead, only the parental phenotypes
(TD and td) are seen. |
| (ii) |
The absence of the non-parental types and the semi-sterility suggest
that the explanation may be a translocation. One possible configuration
is shown:

The "adjacent" pattern of segregation would give Tt and Dd gametes, while the "alternate" pattern would give TD and td. The Tt and Dd gametes would be inviable, so the only viable progeny would have
TD and td phenotypes -- the parental types.
Note that there is more than one configuration that would fit
the results. For example, the t and d alleles need not be on the translocated segment. |
|
| 1. |
The match to the suspect in Case 1 is more meaningful -- the alleles
that are matched are much less frequent in the population, so
a chance match (i.e., the suspect and the crime scene DNA matching
just due to chance) is improbable. In Case 2, the alleles are
more frequent, so a chance match is more probable. One would therefore
feel more confident finding suspect 1 to be guilty than finding
suspect 2 guilty. |
|
The math
Case 1: probability of a chance match = (0.01)(0.02)(0.003)(0.01)(0.07)(0.04)(0.13)(0.08)(0.04)(0.05)32
= 1.1 x 10-14 -- i.e., the probability of getting this combination of alleles
just by chance is about 1 in 100 trillion.
Case 2: probability of a chance match = (0.2)(0.4)(0.15)(0.35)(0.4)(0.3)(0.3)(0.6)(0.2)(0.3)32 = 1.7 x
10-4 -- i.e., a little over 1 in 6000.
(The factor of 32 comes in because there are two ways of getting
each heterozygous combination, and 5 loci we're looking at = 25 = 32.) We'll see more of this factoring-in-2 business when we
get to population genetics.) |
| 2. |
(a) |
Note: Your answer does not need to be this long-winded!
The strategy here is to look at the dominant trait and ask: does
any one allele of the polymorphic trait preferentially segregate
with the dominant trait? (And conversely, does an allele preferentially
segregate with the recessive allele? This question is harder to
address, because in this pedigree there are seven sources of the
recessive allele -- two copies from I-1, one copy from I-2, and
two each from II-1 and II-5 -- so it's harder to track the recessive
allele. In contrast, there's only one source of the dominant trait
-- I-2 -- so it's a lot easier to track.)
The source of the dominant trait in this pedigree is I-1. We know
that he is heterozygous for the dominant trait (because he has
an unaffected daughter, II-3). So if D = dominant and d = recessive, he is Dd. He has alleles 13 and 20 at PS1, and 21 and 27 at PS2. So we can ask if one of these four alleles segregates
with the dominant trait (i.e., do people who show the dominant
phenotype -- and therefore, inherited allele D -- also get one of those four alleles preferentially?)
Let's look at PS1 first. There are 11 affected (Dd) individuals
not counting I-2. Of these, three have inherited allele 13 (II-2, III-3, III-5) and four have inherited allele 20 (II-4, III-10, III-12, III-14). The remainder have inherited neither
13 nor 20 (these individuals have inherited alleles from people
marrying into the family). So allele D of I-2 has co-segregated about half the time with allele 13 of PS1 and about half the time with allele 20. Therefore, PS1 does not appear to be linked to D/d -- the two loci appear to be segregating independently of each
other.
Now let's look at PS2. Here, the alleles in individual I-2 are 21 and 27. Of the eleven Dd progeny, ten also have allele 21; only one has allele 27. Additionally, of the six dd progeny, only one has allele 21; the remainder have other alleles. Therefore, it appears that
in this pedigree, allele 21 is preferentially found with allele D; the two loci (D/d and PS2) are probably linked. In this particular case, I-1 must have allele D and allele 21 of PS2 on the same homologue (in cis, or in "attraction phase"). |
|
(b) |
If we assume that the scenario we have described above is true
-- i.e., D/d and PS2 are linked, with alleles D and 21 in cis -- then we can look for individuals who have allele D but not allele 21, or conversely, lack allele D but have allele 21, as evidence of recombination. Two individuals fit these criteria:
III-6 is affected (Dd) but does not have allele 21, and individual III-9 is unaffected dd, but has allele 21. |
| 3. |
There are 64 possible triplets and three of these (UAA, UAG, UGA)
are stop codons. Therefore, in a random DNA sequence, the chance
of encountering a stop codon in any particular reading frame =
3/64, or about 1 out of every 21 codons. So on average, a ribosome
will encounter a stop codon about 21 codons following a frame
shift; the peptide will be 20 amio acids beyond the point of the
frame shift. |
| 4. |
The fraction of control (sugar-water-treated) crosses that lack
wildtype male progeny is the background rate of spontaneous mutagenesis.
This rate is = 13/(6255 + 13) = 0.002/generation
We can now compare the rate of mutation in the other groups to
see if any treatment causes an increase above this background
rate. Thus --
Food color #1: 76/(4821 + 76) = 0.016/generation -- this rate is higher than the background rate, so Food color
#1 is mutagenic.
Food color #2: 18/(9361 + 18) = 0.002/generation -- this rate is no higher than the background rate, so Food color
#2 is not mutagenic.
Food color #3: 91/(5382 + 91) = 0.017/generation -- this rate is higher than the background rate, so Food color
#3 is mutagenic. |
| 5. |
Ultraviolet light is mutagenic because DNA can absorb photons
in UV wavelengths and thereby undergo chemical reactions that
it otherwise would not. Therefore, the wavelengths of UV light
that are most mutagenic should correspond to those wavelengths
that are best absorbed by DNA -- so the efficiency of mutagenesis
should correspond to the absorption of UV by DNA (the solid red
line in the graph). |
| 6. |
Remember that normal diploid cells have two copies of the gene
for Enzyme E (Gene E) and two copies of the gene for Enzyme Z
(Gene Z). So, assuming that the amount of enzyme in the cell scales
linearly with the gene copy number, each copy of Gene E contributes
30 units of enzyme E activity (so a diploid produces 60 units
of Enzyme E), and each copy of Gene Z contributes 50 units of
Enzyme Z activity. So a cell line that has a duplication of a
gene should produce three copies' worth of enzyme. For Enzyme
E, the duplication should result in cells that produce ~90 units,
and for Enzyme Z, a duplication of the gene should result in ~150
units.
To find the location of Gene E, we look for cell lines that produce
~90 units of Enzyme E, and ask, what's common between these duplications.
We see from the table that cell lines 1, 5, and 6 all produce
~90 units of Enzyme E (while the other cell lines produce the
normal ~60 units). So these three cell lines must have duplications
of Gene E. The band that is common to these three duplicaitons
is band 2 -- that must be the location of Gene E.
For Enzyme Z, cell lines 2 through 6 all produce ~150 units instead
of the standard 100 units. The band common to the duplications
in these lines is band 5; Gene Z must be located there. |
| 7. |
(a) |
We expect the progeny to show the dominant phenotypes. In progeny
showing the recessive traits, the recessive alleles must have
been uncovered by deletions in gametes produced by the X-irradiated
male. |
|
(b) |
Although we could postulate multiple deletions in each progeny
class, the most parsimonious explanation is that each progeny
class has a single deletion that uncovers recessive alleles at
multiple adjacent loci. So if two recessive traits are uncovered,
the genes for those two traits must be next to each other on the
chromosome. Using that logic --
- Strain #1 uncovers a and c, so gene a and gene c must be neighbors
- Likewise, a and b must be neighbors; a must be between b and c (the order so far is b-a-c)
- f is next to c, so the order is b-a-c-f
- de is next to f (but the order of d and e is not known yet)
- and from strain #6, e is next to f, so the completed gene order is b-a-c-f-e-d
|
| Modified from 1998 |
| (a) |
Sectors of different sizes will arise depending on when during
growth of the colony the mutation event occurred--the earlier
the mutation, the larger the sector. Half-sectored colonies reflect
mutations that occurred in the first division of the cell that eventually formed the colony (e.g., if there
was an unrepaired mismatch in Ade+ DNA prior to the first round
of DNA synthesis, replication would lead to one normal daughter
chromosome, which would result in the white sector; and one mutated
daughter chromosome, which would give rise to the red sector). |
| (b) |
The problem in measuring mutation frequency is estimating how
many cell divisions have occurred. However, we do know how many
cells underwent mutations to give sectors in the first division--it
is the number of half-sectored colonies. We also know how many
"first divisions" occurred--it is equal to the number of colonies
on the plate. Therefore, the frequency of mutation = frequency
of mutation in the first division = (# of half sectored colonies)/(total
# of colonies). |
| 1. |
With respect to the disease, the boy must be homozygous recessive
(because achondroplasia is dominant). If A = achondroplasia and a = unaffected, the boy is aa.
With respect to the polymorphic locus, one allele has 12 repeats
of CA, while the other has 7 repeats--so his genotype for the
polymorphic site is 7,12. (Or 12,7.)
Therefore, his overall genotype for these two loci is aa 7,12. |
| 2. |
(a) |
Sample B DNA must be circular -- one cut in a circular DNA molecule
just converts it from circular to linear without dividing it into
smaller fragments. Sample A DNA is either linear (with a single
cut site for Pst I, so that one cut breaks the linear molecule
into two), or circular with two cut sites for (the first cut linearizes
the circle; the second cut breaks the linear molecule into two). |
|
(b) |
The conclusion for Sample A does not change -- since it is cut
into two fragments by Pst I, it must have at least one cut site.
For Sample B, however, if it remains as a single molecule after
Pst I treatment -- so either it is a circle with a single cut
site, as we concluded in (a), or it lacks Pst I cut sites altogether,
in which case we do not have enough information to decide whether
it is circular or linear. |
| 3. |
(a) Note that digests (ii) and (iii) give multiple fragments of
the same size -- depicted here as thick bands. Note that the various
fragment sizes should always add up to the full length (20 kb
in this example). In real life, if you saw two bands that didn't
add up to the full size (e.g., lane ii -- 7 kb band + 3 kb band
= 10 kb instead of 20 kb), that would clue you in that there might
be multiple fragments of the same size. |
(b) The probe will hybridize only to those fragments with which
it overlaps. Again, some bands contain two distinct fragments
of the same size, only one of which (in this case) should be hybridizing
to the probe. |
|
 |
 |
| 4. |
(a) |
The size of the full genome should be the sum of the sizes of
the individual fragments for any given digest -- e.g., in "Ava
I alone" the fragments are 12 kb and 48 kb, so the total size
is 60 kb. You should get the same answer from each digest. |
|
(b) |
Each enzyme by itself gives two fragments. Therefore, each enzyme
must have a single cut site in the bacteriophage genome, such
that each enzyme cuts the DNA into two.
Ava I must be cutting 12 kb from one end (i.e., 48 kb from the
other end); Bam HI cuts 10 kb from one end, and Cla I cuts 18
kb from one end. The question is, which end are we measuring from -- we know that Ava I cuts 12 kb from one
end, but Bam HI might be cutting 10 kb from the other end. To
get that information we look at the double digests.
Let's look at Ava I + Bam HI. We know that Ava I by itself is
going to generate a 12 kb fragment and a 48 kb fragment. We now
see in this double digest that Bam HI leaves the 48 kb fragment
untouched -- we're still seeing a 48 kb fragment. In contrast,
the 12 kb fragment released by Ava I has been cut by Bam HI to
a 10 kb fragment and a 2 kb fragment. Therefore, Bam HI site must
be within the 12 kb Ava I fragment. The map we have so far is:
We can do a similar analysis for Cla I. In the Ava I + Cla I double
digest, we see that Cla I does not cut within the 12 kb AvaI fragment
(because if it had cut within the 12 kb fragment we'd be seeing
smaller-than-12 kb fragments, which we don't). However, Cla I
does cut within the 48 kb Ava I fragment to release a 30 kb fragment
and an 18 kb fragment. We already know that Cla I cuts 18 kb from
one end of the genomic DNA molecule -- therefore there is only
one way to place the Cla I site on the map, as shown:
The map predicts that a Bam HI + Cla I double digest should give
10 kb, 32 kb, and 18 kb fragments -- which according to information
we are given is true. |
| 5. |
(a) |
The primers are :
5'-TGCTCTGGAT-3' and 5'-TCCGAGAGCC-3', which correspond to the yellow, boxed segments (immediately
flankng the greyed segment) below:

|
|
(b) |
The full length will be 46 bp (10 bp for each primer + 26 bp in
the middle). |
|
|
Note added 10/26/99: The way the question is worded, it is actually
possible to amplify an even smaller fragment, by choosing primers within the grayed segment as shown below:

In this case, only the grayed segment would be amplified, giving
a product length of 26 bp. |
| 6. |
(a) |
Someone who is homozygous normal will have two identical copies
of the allele that has all four Xba I sites -- i.e., digestion of their DNA with Xba I and hybridization
with the indicated probe should detect three fragments, of sizes
3 kb, 5 kb, and 7 kb.
In contrast, a carrier (a heterozygote with one normal and one
disease allele) will have one allele that has 4 Xba I sites and
one allele that lacks one or two of the middle Xba I sites (see
table below). Their DNA, when cut and probed similarly, will also
pick up the same three fragments (3 kb, 5 kb, 7 kb) because of
the one normal allele. However, the other allele will give different
products,which will be seen in addition to the normal digestion
products (asterisks indicate absence of Xba I sites):
| Genotype |
Digestion products detected |
 |
3 kb, 5 kb, 7 kb, and 8 kb |
 |
3 kb, 5 kb, 7 kb, and 10 kb |
 |
3 kb, 5 kb, 7 kb, and 15 kb |
|
|
(b) |
As seen above, four different alleles are possible -- the normal
allele (with all 4 Xba I sites) plus the three alleles lacking
one or both Xba I sites. |
|
(c) |
There are 10 possible genotypes -- 4 homozygous and 6 heterozygous
(see Week 1 Q. 10 for an explanation). |
| 7. |
(a) |
The polymorphic site alleles are co-dominant -- both forms are detected when one tests the allele composition
at that site. |
|
(b) |
If the two loci are unlinked, gametes of the different possible
genotypes are equally probable; the eight possible progeny genotypes
are equally possible, as shown below:
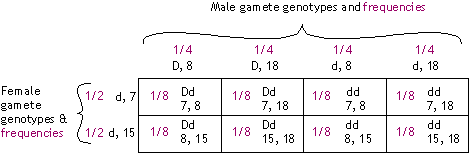
|
|
(c) |
We are not given phase information here -- i.e., we don't know whether allele configuration in the
father is {D 8 & d 18}, or {D 18 & d 8}. (Does the mother's allele configuration matter in this question?)
Different outcomes will be seen depending on the phase, as shown
below. The gametes produced by the mother will be d, 7 and d, 15 in equal proportions, as in (b).
| Phase (allele configuration) in father: |
| {D 8 & d 18} |
{D 18 & d 8} |
|
Gamete genotypes (frequencies):
- D, 8 (0.4)
- d, 18 (0.4)
- D, 18 (0.1)
- d, 8 (0.1)
|
Gamete genotypes (frequencies):
- D, 18 (0.4)
- d, 8 (0.4)
- D, 8 (0.1)
- d, 18 (0.1)
|
 |
 |
|
| 8. |
Because we are assuming complete linkage,we can simply look at
the genotype at the polymorphic locus and assign the disease phenotype
accordingly -- homozygous {30, 30} = affected; heterozygous {30,
42} = unaffected, carrier: |
|
|
| 9. |
(from 1998)
The Lod score graph tells us that the pedigree data favor a map
distance of 5 cM between Gene 1 and PS1; a map distance of 15
cM between Gene 1 and PS2; a map distance of 10 cM between Gene
1 and PS3, etc. A map that is consistent with these interpretations
is: |
|
|
| 1. |
For every crossover between the two loci, two of the four products
of meiosis will be recombinant. Therefore, if 8% of the meioses
have a crossover in that interval, 4% of the products will be
recombinant -- so the map distance is 4 cM. (Go through the worksheet on p.40 of the lecture notes if you're
still confused.) |
| 2. |
AaBb x aabb |
The products are in 1:1:1:1 ratio -- the loci appear to be assorting
independently, so we cannot assign linkage, and cannot determine
the parental configuration. |
|
AaDd x aadd |
Here, AD and ad phenotype progeny greatly outnumber Ad and aD -- so AD and ad must be the parental allelic configurations (A and D are linked in cis). The recombinant types (Ad and aD) account for 8 of 200 = 4% of the progeny; the map distance between
A/a and D/d = 4 cM. |
|
AaFf x aaff |
Af and aF phenotype progeny greatly outnumber AF and af -- so Af and aF must be the parental allelic configurations (A and F are linked in trans). The recombinant types (AF and af) account for 36 of 300 = 12% of the progeny; the map distance
between A/a and F/f = 12 cM. |
|
BbEe x bbee |
Be and bE phenotype progeny greatly outnumber BE and be -- so Be and bE must be the parental allelic configurations (B and E are linked in trans). The recombinant types (BE and be) account for 10 of 210 = 4.8% of the progeny; the map distance
between B/b and E/e = 4.8 cM. |
|
DdFf x ddff |
Df and dF phenotype progeny greatly outnumber DF and df -- so Df and dF must be the parental allelic configurations (D and F are linked in trans). The recombinant types (DF and df) account for 20 of 250 = 8% of the progeny; the map distance
between D/d and F/f = 8 cM. |
|
Putting this information together -- A/a, D/d and F/f are in the
same linkage group; B/b and E/e are in a separate linkage group.
The linkage relationships can be depicted as:
- A D F
- |--------|----------------|
- 4 cM 8 cM
|
- B E
- |---------|
- 4.8 cM
|
|
| 3. |
The parental genotypes are TTFF x ttff to give TtFf. Therefore, the parental genotypes for gametes made by the F1
plants are TF and tf.
If the two loci are unlinked, we expect the four progeny phenotypes (TF, Tf, tF, and tf) in equal proportions. Because there are 1000 proteny total,
we expect 250 of each phenotype if the loci are unlinked.
If the two loci are linked at at map distance of 44 cM, we expect 44% of the gametes to
be recombinant -- i.e., 44% of the progeny should show the recombinant
(non-parental) phenotype. As shown above, the parental types are
TF and tf, so we expect 44% of the progeny to add up to Tf and tF, or 22% each. The parental types then should be 56% of the progeny
= 28% each. So for 1000 progeny, we expect 280 each of TF and tf, and 220 each of Tf and tF.
Clearly, the observed progeny numbers don't match either scenario.
So let's do a chi-square analysis on the two data sets, for the
two sets of expectations, and see if we can find statistical evidence
against either model. |
|
Scenario 1 -- the loci are unlinked
| Phenotype |
Expected (E) |
Observed (O) |
(E-O)2/E |
| Tart, fibrous |
250 |
281 |
3.844 |
| Tart, smooth |
250 |
219 |
3.844 |
| Sweet, fibrous |
250 |
251 |
0.004 |
| Sweet, smooth |
250 |
249 |
0.004 |
|
Chi-square value = |
7.70 |
|
df = |
3 |
The corresponding P value is just over 0.05 -- just above the standard cutoff for
rejecting the null hypothesis (that the deviation from expected
is just due to chance).
|
|
Scenario 2 -- the loci are linked at 44 cM
| Phenotype |
Expected (E) |
Observed (O) |
(E-O)2/E |
| Tart, fibrous |
280 |
281 |
0.004 |
| Tart, smooth |
220 |
219 |
0.005 |
| Sweet, fibrous |
220 |
251 |
4.368 |
| Sweet, smooth |
280 |
249 |
3.432 |
|
Chi-square value = |
7.81 |
|
df = |
3 |
Again, the corresponding P value is just over 0.05.
What does this mean for deciding between the two modes of inheritance?
The statistical analysis tells that the data are consistent (just
barely) with either model -- so we cannot decide between the two
models based on this statistical test.
At least two approaches are possible to settle the question. One
is simply to collect more data (repeat the crosses, count a lot
more progeny) and repeat the statistical analysis in the hopes
that one hypothesis or the other can be rejected with more data.
However, if T/t and F/f are linked, it should be possible to find
genes in the interval between them that are linked to both. That
way, we'd be working at smaller map distances, and thereby have
a better shot at establishing linkage. |
| 4. |
The flaw is that the F1 progeny, although heterozygous for sneezy and jumpy, are homozygous for itchy. So while recombination between sneezy and jumpy can be detected, there's no way to detect recombination involving
itchy.

... no change in genotype (ijs and i++ giving i++ and ijs)
Note: i = itchy, j = jumpy, s = scratchy; only one chromatid of each homolog is shown
He should be using a fully heterozygous (ijs/+++ in any cis/trans configuration) and a homozygous recessive (ijs/ijs) for his mapping cross.
Assuming that we are starting with the dominant alleles in cis
in the heterozygote (i.e., +++/ijs), then parental, double-crossover, and single-crossover products
can be predicted as follows:
| Gamete type |
Gamete genotype ( = progeny phenotype) |
Predicted number of progeny |
| DCO |
i + s and + j + |
= (0.18)(0.12)(1000) = 22 total; 11 of each |
| SCO in i-j interval |
+ j s and i + + |
- = (total recombinants in this interval) - DCO
- = (0.18)(1000) - 22
- = 180 - 22 = 158; 79 of each
|
| SCO in j-s interval |
+ + s and i j + |
- = (total recombinants in this interval) - DCO
- = (0.12)(1000) - 22
- = 120 - 22 = 98; 49 of each
|
| NCO (parental) |
+ + + and i j s |
- = total - (all recombinants)
- = 1000 - (22 + 158 + 98)
- = 722; 361 of each
|
|
| 5. |
Finding the correct gene order
H = Hairy, P = purple, T = Thorny; and lower case denotes the recessive phenotypes.
The parental non-crossover (NCO) allele combinations are Hpt and hPT (these being the most abundant progeny phenotypes), while the
double-crossover (DCO) classes are HPT and hpt. To find the correct gene order, we start with the known NCO
types, and see if a double crossover yields the known DCO types.
If it doesn't, the order must be wrong; we try a different gene
order (the critical information is the gene in the middle). Trial
and error (trying each of the three genes in the middle) establishes
that H must be the middle gene:

- Products of single crossover (SCO) in P-H interval are phT and PHt.
- Products of SCO in H-T interval are pHT and Pht.
-
Now we can start calculating map distances:
- P-H map distance = percent recombinants in this interval
- = (SCO in P-H) + DCO) as percent of total progeny
- = (150 + 132 + 18)/2500 = 300/2500 = 0.12, or 12 cM.
-
- H-T map distance = percent recombinants in this interval
- = (101 + 81 + 18)/2500 = 200/2500 = 0.08, or 8 cM.
-
- The completed map is:
-
- P/p H/h T/t
- |------------|--------|
- 12 cM 8 cM
-
- Coefficient of coincidence = (observed DCO/(Expected DCO)
- Observed DCO = 18
- Expected DCO = (0.12)(0.08)(2500) = 24
- Coefficient of coincidence = 18/24 = 0.75.
|
| 6. |
The important thing to remember is that in order to map the genes,
we need to be able to detect recombination, and that in order
to detect recombination, one of the parents has to be fully heterozygous.
Here, the genes are on the X chromosome -- so that parent by default
has to be the female (the male only has one X -- no recombination
there).
There are a couple of ways of setting this up. One option is to
make the female heterozygous, and to have recessive alleles on
the male's X chromosome. Then the males and females would consist.
To generate heterozygous females, we could cross homozygous dominant
females (+++/+++) with recessive males (abc/Y); the females in
the resulting progeny would be heterozygotes. When these females
are crossed with abc/Y males, the progeny (males and females)
would show the non-recombinant phenotypes (abc and +++) as well
as the 6 recombinant types: a++ and +bc, ab+ and ++c, a+c and +b+.
A different option is to cross the heterozygous females with males
showing the dominant phenotypes (+++/Y). Then the female progeny
would all show the dominant phenotypes, and would be ignored;
the male progeny would get the single X from the female, and show
the same parental and recombinant phenotypes listed above.
For an example -- see Question 1998-2 in Questions from yesteryear. |
| 7. |
The only human chromosome common to all the cell lines making
Enzyme Q is chromosome 8 -- so that must be the chromosome carrying
the gene for Enzyme Q. |
| 8. |
Enzyme G |
- The chromosomes common to cell lines making this protein are:
2 and 9
- Cell line C has chromosome 2 but does not make the protein. Therefore,
the gene for Enzyme G must be on chromosome 9.
|
|
Enzyme AD |
- The chromosomes common to cell lines making this protein are:
5 and 14
- Cell line E has chromosome 5 but does not make the protein. Therefore,
the gene for Enzyme AD must be on chromosome 14.
|
|
Enzyme H |
- The chromosomes common to cell lines making this protein are:
2 and 9
- Cell line C has chromosome 2 but does not make the protein. Therefore,
the gene for Enzyme H must be also be on chromosome 9.
|
|
1998-1
| (a) |
The parents are XoDXoD and XOdY. The cross is outlined below; the children are expected to be
unaffected females and ocular albinism males in 1:1 ratio.

|
| (b) |
Here, we know that the woman is heterozygous for both traits--but
we don't know whether the dominant alleles are in cis (i.e., the
dominant O allele and the dominant D allele on the same homolog)
or in trans (on different homologs). The man in the cross has
the dominant alleles for both loci, so his daughters will all be phenotypically normal. The sons' phenotypes, however,
will depend on which X chromosome they inherit from the woman,
and on whether she has the dominant alleles in cis or in trans.

|
1998-2
|
You just have to realize that because the ratio of phenotypes
is very different in females vs. males, the mode of inheritance
must be sex-linked--specifically, these are X-linked genes. Other
than that, the procedure is the same as above--you use just the
male progeny to follow the recombination that occurred in the
female parent. (If you are confused--DRAW THE CROSS! You know
that the genes are on the X chromosome; you know the parental
genotypes.)
The parental types (most abundant in the male progeny) are s+ sn+ fu and s sn fu+. The DCO products are s+ sn fu+ and s sn+ fu. Therefore, the s locus must be in the middle; the parental types can be re-written
as sn+ s+ fu and sn s fu+.
A single crossover between sn and s would give sn+ s fu+ and sn s+ fu; a single crossover between s and fu would give sn+ s+ fu+ and sn s fu.
Now we can calculate the percent recombinant types for each interval:
- # of crossovers in sn-s interval = SCO (in sn-s) + DCO = (99 +91)
+ (21 + 17) = 228
- Percent recombination in B-A interval = (228/1000)*100 = 22.8
-
- # of crossovers in s-fu interval = SCO (in s-fu) + DCO = (69 +
75) + (21 + 17) = 182
- Percent recombination in A-C interval = (182/1000)*100 = 18.2
-
|
| (a) |
Genotype of female parent = sn+ s+ fu / sn s fu+ (This notation-- a set of alleles, then a slash "/" then another
set of alleles-- is standard notation to show that the first set
of alleles is on one homolog and the second set of alleles following
the slash is on the second homolog.)
Genotype of male parent = sn+ s+ fu+/Y |
| (b) |
Map of the region:
- sn------22.8 cM-------s------18.2 cM----fu
- |---------------------|------------------|
-
|
| (c) |
- Predicted # of DCo products = (0.228)(0.182)1000 = 41
- Observed # of DCO products = 38
- Coefficient of coincidence = 38/41 = 0.927
- Interference = (1 - 0.927) = 0.073.
|
This problem is easily solved. Human chromosomes present in cell
lines that do not have the insulin sequence can be eliminated from our list of
possible candidates. Therefore, any chromosome that is found in
cell lines D, E, or F can simply be crossed out from the list
of possibilities (eliminated candidates shown below as colored-out
boxes).
| Cell line |
Human insulin sequence present? |
Human chromosomes that are present in the cell line |
| A |
Yes |
6 |
7 |
10 |
11 |
14 |
17 |
18 |
20 |
21 |
X |
| B |
Yes |
3 |
5 |
11 |
14 |
15 |
17 |
18 |
21 |
|
|
| C |
Yes |
4 |
5 |
10 |
11 |
12 |
17 |
18 |
21 |
|
|
| D |
No |
8 |
10 |
12 |
15 |
17 |
21 |
X |
|
|
|
| E |
No |
2 |
5 |
6 |
10 |
12 |
18 |
20 |
21 |
X |
|
| F |
No |
17 |
18 |
20 |
|
|
|
|
|
|
|
Of the remaining candidate chromosomes, the only one that is present
in cell lines A, B, and C is chromosome 11. Therefore, the insulin gene must be located on chromosome 11.
1997-4
| (a) |
 I-1 is unaffected, so he must be XGHY. His daughter inherits his X chromosome, so one of her X chromosomes
must be XGH. However, she has a colorblind, hemophilic son, so her other
X chromosome must have both recessive alleles. Therefore, II-1
is XGHXgh. Her husband (II-2) and son (III-1) are both colorblind but not
hemophilic, so they both must be XgHY. III-2 has both disorders; he is XghY. III-3, being colorblind, must be homozygous recessive for the
color vision locus. One chromosome is XgH (the one she got from her father, II-2); the chromosome she got
from her mother (II-1) is either Xgh (if there was no recombination between the two X's in her mother)
or XgH (if there was recombination). Therefore, III-3 is either XgHXgH or XgHXgh. I-1 is unaffected, so he must be XGHY. His daughter inherits his X chromosome, so one of her X chromosomes
must be XGH. However, she has a colorblind, hemophilic son, so her other
X chromosome must have both recessive alleles. Therefore, II-1
is XGHXgh. Her husband (II-2) and son (III-1) are both colorblind but not
hemophilic, so they both must be XgHY. III-2 has both disorders; he is XghY. III-3, being colorblind, must be homozygous recessive for the
color vision locus. One chromosome is XgH (the one she got from her father, II-2); the chromosome she got
from her mother (II-1) is either Xgh (if there was no recombination between the two X's in her mother)
or XgH (if there was recombination). Therefore, III-3 is either XgHXgH or XgHXgh. |
| (b) |
III-1 – his X chromosome, which he got from his mother, is XgH, while his mother is XGHXgh. |
| (c) |
III-3 inherited XgH from her father; she inherited either Xgh or XgH from her mother. The two genes are 3 map units apart, so we expect
3% of the gametes from II-1 to be recombinant. Considering the
phenotype of III-3, the only possible recombinant gamete is XgH; the probability of that is 0.03. Therefore, the probability
that she is H/H is 0.03. Likewise, the probability that she is
H/h is 0.97. Because she does not show the recessive hh phenotype,
there is no chance (p=0) that she is h/h. |
|
| 1. |
(a) |
Haploid number N = 9; so 2N = 18. At metaphase, the chromosome
should each have two sister chromatids, so the total number of
chromatids = 18 x 2 = 36. |
|
(b) |
As in mitosis, there should be two chromatids per chromosome,
i.e., 36 chromatids (but the arrangement of chromosomes will be different from mitosis). |
|
(c) |
In Anaphase I of meiosis, the homologs separate -- so the resulting
daughter cells have only a haploid set of chromosomes each. Therefore,
at meiotic Metaphase II, the number of chromatids = 2 x haploid
chromosome number (N) = 18. |
| 2. |
The diploid form, having two sets of chromsomes, can undergo meiosis.
The haploid form has only one set to begin with, so it cannot
undergo a reductional division. |
| 3. |
(a) |
The homologs have separated -- so it must be meiosis. |
|
(b) |
Sister chromatids have separated, and there is one copy of each
homolog -- so it must be a mitotic division. |
| 4. |
(a) |
- There are three segregating traits here: G/g, A/a, and X/Y. Therefore, there are 23 = 8 possible gamete genotypes:
| GAX |
GaX |
gAX |
gaX |
| GAY |
GaY |
gAY |
gaY |
|
|
(b) |
Since galactosemia and albinism are both recessive traits, the
sperm will have to carry the recessive allele for each trait.
Furthermore, since we are looking for a son, the sperm will have
to be a Y-chromosome bearing one. Therefore, the genotype of the
sperm has to be gaY. |
|
(c) |
We know that the final genotype has to be gaY. Therefore, at anaphase
I, the Y chromosome has to segregate with the homologs carrying
the recessive alleles, as diagrammed:
Note: In the interests of simplicity, crossing over has been ignored
here. Also, the relative sizes of chromosomes and locations of
genes is fictitious. |
| 5. |
(a) |
- Using XH and Xh to represent X chromosomes bearing the normal and hemophilia
alleles, respectively, the six possible matings are:
| XHXH & XHY |
XHXh & XHY |
XhXh & XHY |
| XHXH & XhY |
XHXh & XhY |
XhXh & XhY |
|
|
(b) |
- For the daughter to be a carrier, she must be heterozygous XHXh (if she were XhXh, she would be affected herself, but she would not be considered
a carrier). So another way of stating the question is -- In which
of these matings are all of the daughters heterozygous? Two possible matings could give this result:
- XHXH & XhY
- XhXh & XHY
- Other matings could give heterozygous daughters also -- but the
daughters wouldn't be all heterozygous.
|
|
(c) |
The children's genotypes are XhXh (affected daughter) and XHY (unaffected son). Because daughter received Xh from each parent, the father must be XhY. The mother transmitted one hemophilia allele (to the daughter)
and one normal allele (to the son) -- so she must be a carrier,
XHXh. So the parental genotypes are: XHXh (mother) and XhY (father). |
| 6. |
Affected children have unaffected parents, so the disease cannot
be dominant (assuming complete expressivity and penetrance). Women
and men are affected, so it cannot be sex-limited or Y-linked.
If one assumes that the disease is fairly common, then it could
be autosomal recessive. However, given that there are many more
affected men than affected women, a more probable explanation
is that it is X-linked recessive. Alternatively, it could be sex-influenced
-- dominant in males, but recessive in females. |
| 7. |
Again, affected children have unaffected parents, so the trait
cannot be dominant.
It could be autosomal recessive. If so, however, we would have
to assume that the disease is fairly common, because heterozygotes
would have to enter the pedigree on five separate occasions (I-1/I-2,
II-2, III-8, IV-2, and IV-7). Furthermore, only men have been
affected in theis pedigree, arguing against a simple autosomal
recessive pattern.
The fact that only men are affected in this pedigree suggests
sex-linkage. But affected men have unaffected sons, so it is not
Y-linked. It could be X-linked recessive -- but the trait appears
to be passed on from father to son in one instance (IV-8 to V-6).
So it could be X-linked recessive only if IV-7 is a carrier.
It could also be sex-limited (phenotype expressed in men), but
as with autosomal recessive, we'd have to assume that the disease
is common.
And as with #6, it could be sex-influenced, dominant in males
but recessive in females.
Because it is possible to explain this pedigree either as autosomal
recessive/sex-limited (if the disease is common) or as X-linked
recessive (if the disease is relatively rare), we cannot deduce
anything about how common or rare the disease is from just the
pedigree. We could as a matter of parsimony say that the most
probable mode of inheritance is X-linked recessive or sex-influenced,
but leave open the possibility that it is autosomal recessive
or sex-limited if the disease proves to be common. |
| 8. |
The fact that phenotypes in the F1 are skewed with respect to
sex immediately suggests that the trait must be sex-linked. The
trait is not passed father-to-son (F1 males are normal), so it
cannot be Y-linked. That leaves X-linked inheritance. The F1 males
get their X chromosomes from the parental females. That there
is only one phenotype amongst the F1 males tells us that the parental females must be homozygous for the normal allele. That means that the F1 females must all
be heterozygotes (getting a normal X from the mother and a squiggly-eye
X from the father). But these heteroozygous F1 females are all
squiggly-eyed. Therefore, the squiggly-eye phenotype must be X-linked dominant. |
|
The F1 x F1 cross would give squiggly eye females, squiggly eye
males, normal females, and normal males in 1:1:1:1 ratio, as shown
below:

where S = squiggly-eye and + is normal |
| 9. |
The key here is in realizing that because these are independently
assorting traits, we can look at each trait separately-- |
|
(a) |
The cross here is AABbDdee x AaBbddEe. We are asked to calculate what fraction of the progeny will
have the phenotype ABde. Because these are independently assorting traits, we can calculate
the fraction of progeny that will have phenotype A, then the fraction
that will have phenotype B, etc., then multiply these fractions
to get the fraction that has all the desired phenotypes. Thus --
- AA x Aa --> all the progeny will be phenotype A
- Bb x Bb --> 3/4 of the progeny will be phenotype B
- Dd x dd --> 1/2 of the progeny will be phenotype d
- ee x Ee --> 1/2 of the progeny will be phenotype e
Therefore, the fraction of progeny expected to be phenotype ABde
is (1)(3/4)(1/2)(1/2) = 3/16. |
|
(b) |
Here, we have to find the fraction of progeny that will have the
genotype AabbddEe. Using the same logic as above--
- AA x Aa --> 1/2 of the progeny will be genotype Aa
- Bb x Bb --> 1/4 of the progeny will be genotype bb
- Dd x dd --> 1/2 of the progeny will be genotype dd
- ee x Ee --> 1/2 of the progeny will be phenotype Ee
Therefore, the fraction of progeny expected to be genotype AabbddEe
is (1/2)(1/4)(1/2)(1/2) = 1/32. |
| 10. |
For a dihybrid cross, we expect to see a 9:3:3:1 ratio of phenotypes
in the offspring--clearly not the case here. Because nothing is
mentioned about males vs. females, we have to assume that this
is not a sex-linked gene. To sort out the puzzle, therefore, we
could begin by looking at each phenotype separately and seeing
if that helps.
The observed progeny are creeper white, creeper yellow, normal white, and normal yellow chickens in 6:2:3:1 ratio. Let's look at creeper vs. normal separately
from yellow vs. white. When we do that, we find that the ratio
is 8 creeper : 4 normal , i.e., 2:1 creeper: normal. Hmmm. Where
have we seen a heterozygote x heterozygote cross giving a 2:1
ratio before? That's right, if creeper is dominant over normal
and creeper is lethal when homozygous, we'd get a 2:1 ratio of
creeper : normal in the progeny.
How about white vs. yellow? Here, the ratio is 9 white : 3 yellow,
a simple 3:1 ratio. Therefore, white must be dominant and yellow
is recessive.
Putting it all together, the cross is CcWw x CcWw (where C= creeper, dominant, c= normal, recessive; W = white, dominant, w = yellow, recessive) and CC offspring die:
|
| 11. |
This one is a little tricky. A common mistake is to misinterpret
the question to think that the first two children are boys --
when in fact, all we know is that at least two children (in any order) are boys. If the sex of the children is written
in order of birth as B (for boy) or G (girl), the possible 3-children
families with at least 2 boys are:
- BBG
- BGB
- GBB
- BBB
Only one of the four possible sets has all three children being
boys -- so if you know that two of the children are boys, the
probability that all three are boys is 1/4. |
| 12. |
We use the binomial distribution to solve this one. Because this
is a recessive disorder, and both parents are heterozygous, the
probability of an affected child is 1/4. Therefore, let a = probability
of unaffected child = 3/4, and b = probability of affected child
= 1/4.
The equation then is
- (a+b)6 = 1
- a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6 = 1
For a family with exactly 2 affected and 4 unaffected children,
we use the term 15a4b2 (the exponents indicating the number of a=unaffected and b=affected
children). Substituting the probabilities of unaffected and affected
children, we get:
p(2 affected children) = 15a4b2 = 15(3/4)4(1/4)2 = 1215/4096 = 0.297.
- For the probability of at least two affected children, we could
use:
- 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6
But an easier way is to find the probability of less than two
affected children, then subtract that value from 1 --
- p(at least 2 affected) = (1 - p(less than 2 affected))
- = 1 - (a6 + 6a5b)
- = 1 - ((3/4)6 + 6(3/4)5(1/4))
- = 1909/4096 = 0.466
(Try it. The longer expression 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6 will give the same result.) |
| 13. |
(a) |
This being a dihybrid cross, we expect a 9:3:3:1 ratio of tall
purple : tall white : short purple: short white. For 3200 progeny,
the expected numbers are:
- Tall, purple: 3200(9/16) = 1800
- Tall, white: 3200(3/16) = 600
- Short, purple: 3200(3/16) = 600
- Short, white: 3200(1/16) = 200
|
|
(b) |
| Phenotype |
Expected (E) |
Observed (O) |
(E-O)2/E |
| Tall, purple |
1800 |
1784 |
0.142 |
| Tall, white |
600 |
620 |
0.67 |
| Short, purple |
600 |
612 |
0.24 |
| Short, white |
200 |
184 |
1.28 |
|
Chi-square value = |
2.332 |
|
df = |
3 |
For df = 3 (i.e,. three degrees of freedom) the chi-square = 2.332,
the P value is just over 0.5, which is well above the standard
cut-off of 0.05 for rejection of the null hypothesis. Therefore,
the null hypothesis (that the deviation from expected values is
just due to chance) cannot be rejected. |
| 14. |
What are the possibilities here?
Possibility # 1: the cross was homozygous purple x homozygous purple; there should be no white-flower progeny
Possibility #2: the cross was heterozygote x heterozygote; 1/4 of the progeny should make white flowers.
If the seed merchant picks just one seed at random and grows it
up, and it makes white flowers -- she knows it must have been
a heterzygote x heterozygote cross. However, if she picks one
seed, and it makes a purple-flower plant -- can she then say that
it must have been a homozygote x homozygote cross? No, because
even in a heterozygote x heterozygote cross, 3/4 of the progeny
will be purple, so she has a 3/4 chance of picking a purple progeny
even if white progeny are present--i.e., she has a 1/4 (=0.25)
probability of missing a white progeny.
Suppose she picks two seeds? Then the probability that both will
be purple (if it was indeed a dihybrid cross) = (3/4)(3/4) = 9/16;
the probability that she has missed a white progeny plant has
dropped to 7/16 = 0.4375. So that's the question -- how many seeds
should she sample if she wants the probability of accidentally
missing a white-flower seed to drop below 2%. In other words,
she needs to sample n seeds such that
(3/4)n = 0.02
or, n(log(0.75)) = log(0.02)
n = 13.6
So if she samples 14 seeds and they all grow up to make purple
flowers, there is < 2% probability that white flower seeds are
present but missed just due to chance. |
| 15. |
To know the probability that IV-1 will be affected, we need to
know the genotypes of the parents, III-4 and III-5. In turn, we
have to know the genotypes of their parents, and so on.
Because I-1 and I-2 are unaffected but have an affected daughter
(II-1), they must both be carriers -- genotype Dd (where D = dominant,
unaffected; d = recessive, affected). II-3 is D_, with a 1/3 chance
of being DD and 2/3 chance of being Dd. II-5 and II-6 are both
Dd (because they are unaffected but have an affected son, III-9).
III-4 is unaffected; the only way she can have an affected child
is she is heterozygous Dd. What is the probability of that? She
(III-4) has a father who is DD and a mother who has a 2/3 chance
of being Dd. Therefore, the probability that III-4 is Dd is (1/2)(2/3)
= 1/3. Likewise, III-5 has to be heterozygous Dd for their child
to be affected. The probability that III-5 is heterozygous Dd
is 2/3 (he could be DD or Dd, with a 2/3 chance of being Dd --
just as with II-3).
Therefore, the chance that they will have an affected child =
(1/4)(1/3)(2/3) = 1/18. |
|
Answers to selections from 1998
1998-1
(i) The disease is probably not autosomal recessive--there are
several instances where people marrying into the family have affected
children; the people marrying in would all have to be heterozygotes,
an improbably scenario.
(ii) The pedigree is fully consistent with autosomal dominant where I-1 is heterozygous and 1-2 is homozygous normal, as is
everyone marrying into the family.
(iii) X-linked recessive can be ruled out, because affected females
have unaffected fathers (e.g., II-1, IV-3).
(iv) X-linked dominant can be ruled out also, because affected
men have unaffected daughters (who would inherit the X chromosome
carrying the dominant disease allele from the father).--e.g.,
II-5.
(v, vii) Males and females are affected, so the disease is not
Y-linked or sex-limited.
(vi) With sex-influenced inheritance, there are two possibilities--dominant
in males and recessive in females, or dominant in females and
recessive in males. Affected women have unaffected sons (e.g.,
I-1 and II-3), so it cannot be recessive in women and dominant
in men. Likewise, affected men have unaffected daughters (e.g.,
II-5 and III-6) so it cannot be dominant in women and recessive
in men.
Thus, the mode of inheritance that best explains the observed
pedigree is autosomal dominant.
- 1998-2
- The disease skips generations, so it is not dominant. The disease
being rare, it is unlikely to be autosomal recessive--it would
require heterozygotes marrying into the family on at least two
occasions. Males and females are affected, so it is not Y-linked
or sex-limited. It cannot be sex-influenced, because unaffected
parents have affected children. It cannot be X-linked recessive,
because an affected daughter has an unaffected father (from whom
she got an X). That leaves us with either the rare possibility
of heterozygotes marrying in (for autosomal recessive), or some
aberrant event, or some mode of inheritance we haven't considered
yet.
1998-3
As described in lecture (refer to the part on evidence for random
segregation of homologs in meiosis), meiosis in the exceptional
females (XXY, homozygous for the X-linked white allele) can give
four kinds of gametes because the two X chromosomes can pair up
during synapsis, or an X and a Y--in which case the lone X could
segregate either with the other X or with the Y. Some of these
eggs can give rise to fertile red-eyed males and white-eyed females,
the secondary exceptions.
NOTE: The grid above shows only the kinds of progeny that can be formed, not the relative numbers. Because
synapsis of the two X chromosomes is more probable than synapsis
of an X with a Y, the "Y is unpaired" outcome of meiosis I (see
the diagram above) is more probable than the "X is unpaired" outcome.
Therefore, gamete types 1 and 2 are much more abundant than gamete
types 3 and 4, and the progeny numbers are skewed accordingly.
1998-4
Because this is a heterozygote x heterozygote cross (normal =
dominant, albino = recessive), we expect to see normal and albino
children in 3:1 ratio-- i.e., the probability of a normal child
is 3/4, and the probability of an albino child is 1/4.
(a) The probability of the outcome described = (3/4)(3/4)(1/4)(1/4)(1/4) = 9/1024
(b) The probability of 2 normal and 3 albino children in any order
can be calculated using binomial expansion. Let a = p(albino) = 1/4 and b = p(normal) = 3/4; since there are five children, the equation
to use is:

The term representing the probability of 3 albino and 2 normal
children is 10a3b2. Substituting the values of a and b, we get:
p(3 albino, 2 normal) =
10(1/4)3(3/4)2 = 45/512 = 0.088
(c) The probability that all five will be normal is:
(3/4)5 = 243/1024 = 0.237
(d) p(at least one albino) = 1 - p(no albino) =
(1 - (243/1024)) = 781/1024 = 0.763
|
| 1. |
(a) |
- True-breeding tall = TT
- True-breeding short = tt
- TT x tt --> Tt heterozygous tall plants in F1.
|
|
(b) |
- The F1 plants are Tt heterozygotes (see above); the cross is as shown:
 As seen from the F2 genotype ratio, half the progeny should be
Tt heterozygotes, and half homozygotes (TT and tt). Therefore, if there are 1000 F2 progeny, 500 of them should
be homozygous (TT or tt) -- i.e., true-breeding. As seen from the F2 genotype ratio, half the progeny should be
Tt heterozygotes, and half homozygotes (TT and tt). Therefore, if there are 1000 F2 progeny, 500 of them should
be homozygous (TT or tt) -- i.e., true-breeding.
-
|
|
(c) |
 Because this is a test-cross, the known parent must be homozygous
recessive (tt). The F1 consist of tall plants only, so the unknown must be
homozygous TT; the cross is shown. (See below for why it can't be heterozygous
Tt.) Because this is a test-cross, the known parent must be homozygous
recessive (tt). The F1 consist of tall plants only, so the unknown must be
homozygous TT; the cross is shown. (See below for why it can't be heterozygous
Tt.) |
|
(d) |
Tt x tt --> 1:1 Tt tall and tt short plants expected. |
| 2. |
(a) |
- The parents and progeny are tall; the only crosses that would
give this result are:
- TT x TT --> TT tall F1 plants
- or
- TT x Tt --> TT (tall) and Tt (tall) F1 plants
|
|
(b) |
- Tall and short progeny are seen in 3:1 ratio, indicating that
the cross must be a heterozygote x heterozygote monohybrid cross:
- Tt x Tt --> Tall and short plants in 3:1 ratio (1 TT tall : 2 Tt tall: 1 tt short).
|
|
(c) |
- Tall and short progeny are seen in 1:1 ratio; this must be a heterozygote
x homozygous recessive cross as in 1(d) above:
- Tt x tt --> Tt (tall) and tt (short) in 1:1 ratio
|
|
(d) |
- The progeny are tall only; as in 1(c), the cross must be
- TT x tt --> Tt (tall)
|
|
(e) |
- Short plants must be homozygous recessive (tt); therefore, the cross is
- tt x tt --> tt short plants only
|
| 3. |
The only way a tall plant can yield short progeny after selfing
(i.e., mating with itself) is if the tall plant is heterozygous.
Therefore, what the question is asking is: what fraction of the
tall plants are heterozygous? (Refer to the crosses shown in answer 2 for these questions.)
Note: You are not looking for tall plants that give only short progeny upon selfing (is that even possible?)--you are
looking for tall plants that will give any short progeny on selfing. |
|
(a) |
If the parental cross is TT x TT, the resulting tall plants will all be TT homozygotes (see 2a); therefore, none of these plants should yield short plants upon selfing. If the
cross is TT x Tt, the progeny are TT and Tt plants in equal proportions, so half of these progeny will yield
short plants upon selfing. |
|
(b) |
The tall progeny in this cross are 1 TT : 2 Tt. Thus, 2/3 of the progeny are heterozygous and will give short
progeny upon selfing. |
|
(c) |
Here, the progeny are Tt (tall) and tt short--all the tall progeny are heterozygous, and should all
give short plants upon selfing. |
|
(d) |
The progeny are all Tt; all of them should give short plants upon selfing. |
| 4. |
 F = free-hanging earlobes, f = attached earlobes. In the two couples
in generation I, we don't know which individual has free earlobes
and which has attached, so I have chosen to display them as sex-unspecified
(but one member of each couple with attached earlobes). The child
in generation III is again sex-unspecified, but has attached lobes
and must therefore be homozygous recessive ff. The parents in
generation II must be heterozygous Ff. F = free-hanging earlobes, f = attached earlobes. In the two couples
in generation I, we don't know which individual has free earlobes
and which has attached, so I have chosen to display them as sex-unspecified
(but one member of each couple with attached earlobes). The child
in generation III is again sex-unspecified, but has attached lobes
and must therefore be homozygous recessive ff. The parents in
generation II must be heterozygous Ff. |
| 5. |
(a) |
- FF x ff
- FF x Ff
- Ff x Ff
- Ff x ff
|
|
(b) |
- FF x ff --> Ff only -- i.e., 100% of progeny are heterozygotes
|
|
(c) |
FF x ff |
|
(d) |
- FF x Ff --> FF and Ff
- Ff x ff --> Ff and ff
|
|
(e) |
Ff x Ff --> FF, Ff, and ff |
| 6. |
(a) |
- The normal parent is homozygous. If the normal wing phenotype
were dominant, the progeny would all show the normal phenotype.
However, there are curly-wing flies in the progeny. Therefore,
curly-wing (C) must be dominant over normal wing (c). Furthermore, two phenotypes (curly and normal) are seen in
the F1, and in 1:1 ratio; therefore, the curly-wing parent must
be a heterozygote. The cross can be depicted as:
- Cc x cc --> Cc and cc in 1:1 ratio
|
|
(b) |
- The cross is:
- Cc x Cc --> 1 CC : 2 Cc : 1 cc
- Of these, the homozygous curly (CC) progeny die, leaving 2 Cc : 1 cc. The true-breeding (homozygous) progeny therefore make up 1/3
of the survivors.
|
| 7. |
Single-stranded -- for a double-stranded DNA molecule (where every
A is paired to a T and every C to a G) the ratio should be 1.0. |
| 8. |
- Here, the ratio of (A+G) to (C+T) = 1; therefore this is proabably
(but not necessarily) double-stranded. Assuming that to be the
case, if C = 19%, G = 19% also.
- So (A+T) = 100 - (C+G) = 62%
- T = 62/2 = 31% (because A = T and A+T = 62%).
|
| 9. |
Two T alleles, 2 t alleles. |
| 10. |
- Abbreviating the alleles as A, S, E, and C--
- There are 10 allele combinations:
| AA |
SS |
EE |
CC |
| AS |
SE |
EC |
|
| AE |
SC |
|
|
| AC |
|
|
|
- Four of them (the top row) are homozygous.
|
|
|
|
Answers to selections from 1998
The simplest approach is a trial-and-error method: interpret each
cross one at a time, and see if your interpretation is consistent
with the interpretation of the previous crosses. To begin with,
it is clear that there are three phenotypes, so just for simplicity,
I am going to assign them 3 allele designations (R, B, W, for
Red, Blue, and White) and assume that they are alleles of the
same determinant. I may have to revise this initial hypothesis
later on--e.g., this may be a case of incomplete dominance between
two alleles--but at least for starters, I'm going to assume simple
dominant/recessive interactions.
Cross (a) -- Red #1 selfed -- yields a 3:1 ratio of red and blue-flowered
plants in the progeny. This looks like a typical heterozygous
F1 cross, with R being dominant and B recessive. So I'm tentatively assigning Red #1 a genotype of
RW.
Cross (b) -- Red #2 selfed -- similarly suggests that R is dominant over W; the genotype would be RW.
Cross (c) -- Blue selfed -- gives a 3:1 ratio of blue:white; blue
must be dominant over white and the genotype of the blue-flowered
plant must be BW.
At this point, we have a hypothesis for all of the genotypes:
- Red #1 = RB
- Red #2 = RW
- Blue = BW
- White = WW (because it is recessive to both others)
We are now in a position to predict the results of the remaining crosses, and seeing if our predictions
are met.
Cross (d) -- Red #1 x Red #2 = RB x RW:
|
R |
B |
| R |
RR (red) |
RB (red) |
| W |
RW (red) |
BW (blue) |
-- a 3:1 ratio of red- to blue-flowered, which is in fact the
observed result.
Cross (e) -- Red #1 x Blue -- should be RB x BW, which should give a 1:1 ratio of red:blue (draw Punnett squares
if you're uncertain about this). Again, that's what we see.
Cross (f) -- BW x WW should give 1:1 blue and white
Cross (g) -- WW x WW gives only white-flowered progeny.
So our initial hypothesis appears to be sound as far as we can
tell from the data provided. We can predict the results of cross
(h):
Red #2 x blue = RW x BW:
|
R |
W |
| B |
RB (red) |
BW (blue) |
| W |
RW (red) |
WW (white) |
-- a 2 : 1 : 1 ratio of red : blue : white.
AO x BO
|


 This is an example of recessive epistasis. The fact that homozygous
B and homozygous O rats could generate AB progeny, and the fact that the F2 progeny fractions are in sixteenths,
tells us that this is a dihybrid cross--i.e., a second gene is
involved in addition to the IA/IB/IO (hereafter abbreviated A/B/O) gene. The A allele, which manifests itself in the F1, must have been present
in homozygous form in the O parent, but masked by the effect of the second gene, thereby
giving an O phenotype. (Why homozygous? Because if it were heterozygous, the F1 progeny
would show other phenotypes besides AB. Likewise, the A allele could not have been hiding in the B parent, because then the B parent would not be true-breeding.) Furthermore, it must be the recessive allele of the second gene (which we shall call h, the dominant allele being H) that prevents expression of the A/B allele. (Why? Because if masking allele were dominant, F1 progeny would
all express the masking phenotype, and would all be O.) The recessive h allele is epistatic to A and B. Thus, the B parent is BBHH and shows the B phenotype; the O parent is AAhh, which does not express the A allele and appears to be O. The F1 progeny are ABHh, and express both A and B alleles. One quarter of the F2 progeny are homozygous recessive
(hh); these again appear to be O because the H allele is required for expression of A and B.
This is an example of recessive epistasis. The fact that homozygous
B and homozygous O rats could generate AB progeny, and the fact that the F2 progeny fractions are in sixteenths,
tells us that this is a dihybrid cross--i.e., a second gene is
involved in addition to the IA/IB/IO (hereafter abbreviated A/B/O) gene. The A allele, which manifests itself in the F1, must have been present
in homozygous form in the O parent, but masked by the effect of the second gene, thereby
giving an O phenotype. (Why homozygous? Because if it were heterozygous, the F1 progeny
would show other phenotypes besides AB. Likewise, the A allele could not have been hiding in the B parent, because then the B parent would not be true-breeding.) Furthermore, it must be the recessive allele of the second gene (which we shall call h, the dominant allele being H) that prevents expression of the A/B allele. (Why? Because if masking allele were dominant, F1 progeny would
all express the masking phenotype, and would all be O.) The recessive h allele is epistatic to A and B. Thus, the B parent is BBHH and shows the B phenotype; the O parent is AAhh, which does not express the A allele and appears to be O. The F1 progeny are ABHh, and express both A and B alleles. One quarter of the F2 progeny are homozygous recessive
(hh); these again appear to be O because the H allele is required for expression of A and B. 








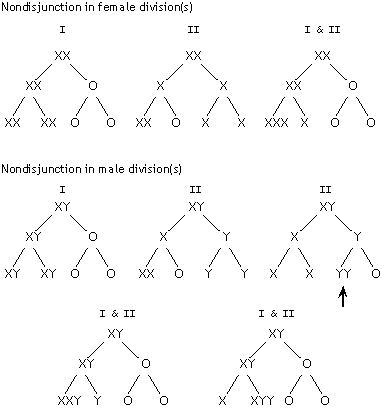










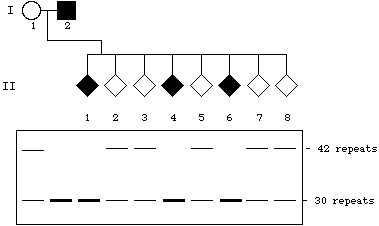



 I-1 is unaffected, so he must be XGHY. His daughter inherits his X chromosome, so one of her X chromosomes
must be XGH. However, she has a colorblind, hemophilic son, so her other
X chromosome must have both recessive alleles. Therefore, II-1
is XGHXgh. Her husband (II-2) and son (III-1) are both colorblind but not
hemophilic, so they both must be XgHY. III-2 has both disorders; he is XghY. III-3, being colorblind, must be homozygous recessive for the
color vision locus. One chromosome is XgH (the one she got from her father, II-2); the chromosome she got
from her mother (II-1) is either Xgh (if there was no recombination between the two X's in her mother)
or XgH (if there was recombination). Therefore, III-3 is either XgHXgH or XgHXgh.
I-1 is unaffected, so he must be XGHY. His daughter inherits his X chromosome, so one of her X chromosomes
must be XGH. However, she has a colorblind, hemophilic son, so her other
X chromosome must have both recessive alleles. Therefore, II-1
is XGHXgh. Her husband (II-2) and son (III-1) are both colorblind but not
hemophilic, so they both must be XgHY. III-2 has both disorders; he is XghY. III-3, being colorblind, must be homozygous recessive for the
color vision locus. One chromosome is XgH (the one she got from her father, II-2); the chromosome she got
from her mother (II-1) is either Xgh (if there was no recombination between the two X's in her mother)
or XgH (if there was recombination). Therefore, III-3 is either XgHXgH or XgHXgh.



 As seen from the F2 genotype ratio, half the progeny should be
Tt heterozygotes, and half homozygotes (TT and tt). Therefore, if there are 1000 F2 progeny, 500 of them should
be homozygous (TT or tt) -- i.e., true-breeding.
As seen from the F2 genotype ratio, half the progeny should be
Tt heterozygotes, and half homozygotes (TT and tt). Therefore, if there are 1000 F2 progeny, 500 of them should
be homozygous (TT or tt) -- i.e., true-breeding.
 Because this is a test-cross, the known parent must be homozygous
recessive (tt). The F1 consist of tall plants only, so the unknown must be
homozygous TT; the cross is shown. (See below for why it can't be heterozygous
Tt.)
Because this is a test-cross, the known parent must be homozygous
recessive (tt). The F1 consist of tall plants only, so the unknown must be
homozygous TT; the cross is shown. (See below for why it can't be heterozygous
Tt.) F = free-hanging earlobes, f = attached earlobes. In the two couples
in generation I, we don't know which individual has free earlobes
and which has attached, so I have chosen to display them as sex-unspecified
(but one member of each couple with attached earlobes). The child
in generation III is again sex-unspecified, but has attached lobes
and must therefore be homozygous recessive ff. The parents in
generation II must be heterozygous Ff.
F = free-hanging earlobes, f = attached earlobes. In the two couples
in generation I, we don't know which individual has free earlobes
and which has attached, so I have chosen to display them as sex-unspecified
(but one member of each couple with attached earlobes). The child
in generation III is again sex-unspecified, but has attached lobes
and must therefore be homozygous recessive ff. The parents in
generation II must be heterozygous Ff.