Introduction to Tribology – Friction
The science of Tribology (Greek tribos: rubbing) concentrates on Contact Mechanics of Moving Interfaces that generally involve energy dissipation. It encompasses the science fields of Adhesion, Friction, Lubrication and Wear.
Leonardo da
Vinci (1452-1519)) can be named as
the father of modern tribology. He studied an incredible manifold of
tribological subtopics such as: friction, wear, bearing materials, plain
bearings, lubrication systems, gears, screw-jacks, and rolling-element
bearings. 150 years before Amontons' Laws
of Friction were introduced, he had already recorded them in his
manuscripts. Hidden or lost for centuries, Leonardo da Vinci's manuscripts were
read in
To the pioneers in tribology one counts besides Leonardo da Vinci also Guillaume Amontons (1663-1705), John Theophilius Desanguliers (1683-1744), Leonard Euler (1707-1783), and Charles-Augustin Coulomb (1736-1806). These pioneers brought tribology to a standard, and its laws still apply to many engineering problems today. Some of their findings are summarized in the following three laws:
1.
The force of
friction is directly proportional to the applied load. (Amontons 1st
Law)
2.
The force of
friction is independent of the apparent area of contact. (Amontons 2nd
Law)
3.
Kinetic friction
is independent of the sliding velocity. (Coulomb's Law)
These three laws were attributed to dry friction only, as it has been well known since ancient times that lubrication modifies the tribological properties significantly. However, it took quite a long time until lubrication was studied pragmatically and lubricants were not just listed such as a "cooking formula". It was Nikolai Pavlovich Petrov and Osborne Reynolds around 1880, who recognized the hydrodynamic nature of lubrication, and introduced a theory of fluid-film lubrication. Still today, Reynolds' steady state equation of fluid film lubrication
![]()
is valid for hydrodynamic lubrication of thick films (> mm) where the frictional (drag) force, F, is proportional to both the sliding velocity, v, and the bulk fluid viscosity h, and inversely proportional to the film lubricant thickness, D. The hydrodynamic theory breaks down below a critical thickness threshold that is expressed in the Stribeck-Curve (Richard Stribeck 1902).
In the twentieth century the theories of dry friction and lubricated friction were further developed. Solid-like behavior of lubricants in the ultrathin film regime (> mm) led to theory of Boundary Lubrication, which was proposed by W.B. Hardy (1919). The adhesion concept of friction for dry friction, already proposed by Desanguliers, was applied with great success by Bowden and Tabor to metal-metal interfaces.
Adhesion is a term relating to the force required to separate two bodies in contact with each other. Desanguliers (1734) proposed adhesion as an element in the friction process, a hypothesis which appeared to contradict experiments because of the independence of friction on the contact area (Amontons 2nd Law). Therefore the tribologists rejected Desanguliers' proposal and devoted their attention to a more geometrical hypothesis of friction, the interlocking theory of mechanical asperities. The contradiction between the adhesive issue and Amontons 2nd Law cleared up by the introduction of the concept of the real area of contact. The real area of contact is made up of a large number of small regions of contact, in the literature called asperities or junctions of contact, where atom-to-atom contact takes place. Bowden and Tabor (1954) showed that the force of static friction between two sliding surfaces is strongly dependent on the real area of contact. A very important outcome of their work, which led to the asperity contact theory of friction, is their detailed discussion about adhesive wear. In contrast to abrasive wear which applies to the form of wear arising when a hard, rough surface slides against a softer surface, in adhesive wear, asperity junctions plastically deform above a critical shear strength, which depends on the adhesive forces of the two surfaces in contact. Assuming during a frictional sliding process a fully plastic flow situation of all asperities, friction is found to change linearly with the applied load as demanded by Amontons 1st Law.
Bowden and
Tabor investigated friction also from the perspective of a purely elastic
sliding process. They used a simplified single asperity model of contact based
on the Hertzian elastic theory, and found
a non-linear friction-load dependence (F=L2/3), which clearly
contradicted Amontons 1st Law and the experiments conducted at that
time. It was Archard (1953), who recognized that there was no contradiction
between an elastic single asperity model and Amontons 1st law that
is based on a contact that involves many asperities. Instead of assuming a
constant number of asperities as Bowden and Tabor did, Archard assumed a load
dependent number of asperities. With this assumption the controversy between
the elastic multiple asperity hypothesis and Amontons 1st Law could
be resolved.
Reynolds fluid film lubrication bases strongly on the assumption that no slip occurs at the fluid solid interface. The condition of no-slip, today described by physical adsorption, brought Hardy to the idea of boundary lubrication. The boundary lubrication is only of molecular thickness. In most cases the lubricant thin film, which acts like a soft solid lubricant, shows incomplete coverage. Wear occurs at these breakthroughs exhibiting complex friction-load dependences. The term boundary lubricant is used for thin organic layer lubricants which can reduce the coefficient of friction by a factor of 20, and the rate of wear by 10,000 or more. Thermodynamic activation models based on Eyring's cage model have been used to describe the frictional phenomena in boundary lubrication of Langmuir Blodgett films (Briscoe, Evans: 1981), and simple fluid lubrication such as hexadecane (He, Overney: 2000).
The shear properties of thin fluid layers under external compressions have found great interest over the last two decades. Surface forces apparatus (SFA) studies, pioneered by Tabor, Israelachvili, McGuiggan and Gee, showed liquids to behave like solids, i.e., cable of storing energy. Interestingly, liquids under these conditions exhibit very high viscosities but unexpectedly low shear resistances.
Issues in Classical Tribology
1. Interlocking Theory – Static and Dynamic Friction
The first mathematical approach to tribology was undertaken by Leonard Euler (1707-1783) with a geometrical resistance theory of "dry" friction – the Interlocking Asperity Theory. Euler's theory provides two terms for static and dynamic friction. The static friction coefficient is provided by the tangent of the asperity angle, i.e., m=tana, while the dynamic friction coefficient is reduced by the kinetic term 2s/gt2cosa (see below).
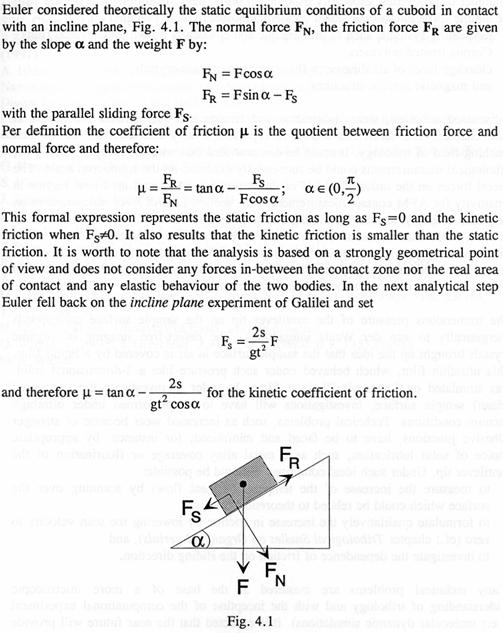
2. Rolling Friction
Ideally rolling contact should offer no resistance to motion, but in reality energy is dissipated in various ways. The sources of energy dissipation may be classified into (Johnson, Contact Mechanics, p. 306 Cambridge Univ. Press (1985))
(a) those which arise through micro-slip and friction at the contact interface
(b) those which are due to inelastic properties of the material, and
(c) those due to roughness of the rolling surfaces.
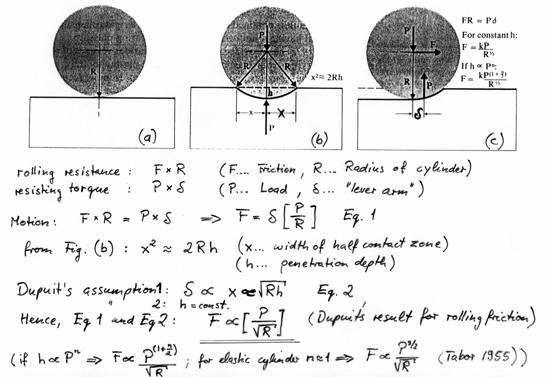
Charles-Augustin
Coulomb (1736-1806) proposed that the frictional resistance of a rolling wheel
or cylinder is proportional to the load P, and inversely proportional to the
radius of the wheel. Coulomb's description of rolling friction entirely
neglected the material compliance. It was Arsène Dupuit in 1840 who argued that
the material behind a rolling cylinder would not fully recover after
deformation. Thus, a simple torque balance (see below) between the interfacial rolling resistance and the material resisting torque leads to an
inverse square root dependence of friction in R. (The rolling resistance is comprised of the product between friction
force, F, and cylinder radius, R. The resisting torque is considering the
applied load, P, with its lever arm d, in which the asymmetric compliance of the
material is reflected.) Dupuit's inverse square root relationship of
rolling friction with the radius of an elastic cylinder was experimentally confirmed
by Tabor in 1955 (see below).[1]
Dupuit's Torque Balance: Determination of the Rolling Friction
Resistance:
3. Inelastic Adhesion Concept of Friction
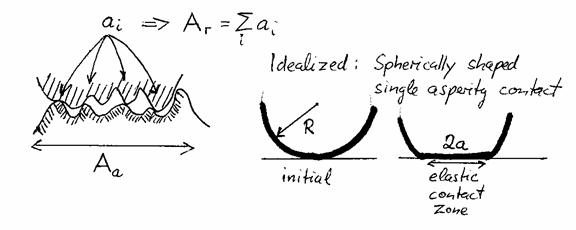
Bowden and Tabor (1954) realized that the old conflict between Desanguliers' adhesive model of kinetic friction and Amontons' law originated in the definition of the contact. Considering that the classical frictional law of Amontons was based on the projected area (apparent area), Bowden and Tabor were concerned with the real area over which the two sliding bodies are in contact. The real area of contact is made up of a large number of small regions of contact, in the literature called asperities or junctions of contact, where atom-to-atom contact takes place. The figure below depicts the situation for (a) a general contact with multiple contact zones with contact area ai, and a total real contact area of Ar=Sai, and a projected (apparent) area Aa, and (b) and idealized single asperity contact with contact radius a.
The contact radius can be determined with the Hertz theory assuming that it is much smaller than the radius of curvature of the asperity, R. The theory yields: «
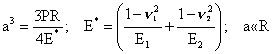
where Ei and vi (i=1,2) represent the Young's modulus and Poisson ratio, respectively, of the bodies in contact. P is the load applied.
The kinetic friction coefficient is by definition the ratio of the friction force and the applied load, i.e., m=F/P. The friction force can be expressed as the product between an interfacial stress, s, that has to be overcome in order to slide, and the actual contact area Ar. The load can be described with the mean pressure of contact pm, multiplied with Ar (for the idealized spherical shape contact, pm=L/pa2). Bowden and Tabor assumed that in order for the bodies to slide relative to each other
(a) the asperities are plastically deformed; i.e., the mean pressure corresponds to about three times the yield pressure, Y, of the material, i.e., pm,crit @ 2.8 Y, and
(b) the interfacial stress component corresponds to the shear strength of the soft material scrit.
Consequently the friction coefficient can be expressed as the ratio between the shear strength of the softer material and about three times the yield pressure; i.e.,
![]() .
.
Notice that Bowden and Tabor's inelastic adhesive theory provides a constant kinetic friction coefficient as proposed by Amontons.
4. Magnitude of the Dynamic Friction Coefficient
It has been found that friction shows in most practical applications an obvious loading dependence. Recently however, in the realm of boundary lubrication, friction was found to be not as dependent on load as expected. This rather unexpected finding can be understood if one considers the total stress, s, as comprised of the intrinsic material shear strength, so, plus the compression stress apm; i.e.,
![]() .
.
As introduced by Bowden and
Tabor, the friction force F = sAr.
For large a the compression term
dominates, and hence, friction is clearly loading P dependent with ![]() . For small a values,
as it is found for boundary lubricants,
. For small a values,
as it is found for boundary lubricants, ![]()

5. Archard's Elastic Model of Friction
In contrary to Bowden and Tabor who assumed fully plastic deformation of the asperities, Archard suggested friction can also occur if the asperities are only elastically deformed. Utilizing the same equation as Bowden and Tabor used (see above, with the exception that the shear stress t is used instead of the compression stress s) and combining them with the Hertzian formalism for the contact radius a, the friction force is found to be proportional to the 2/3-power of the load P, i.e., [2]
![]() .
.
Archard's model has been
experimentally confirmed in SFM single asperity experiments. The contradiction
with Amonton's linear friction-load law is resolved if one considers a loading
dependent asperity number distribution.