Research Projects & Publications

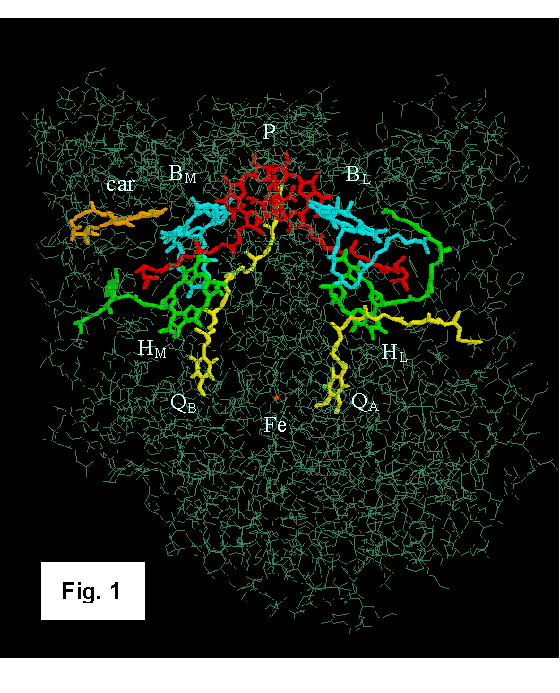
Charge Separation in Photosynthetic Reaction Centers

Reaction centers (RCs) are pigment-protein complexes that carry out the initial photochemical electron-transfer reactions of plants and photosynthetic bacteria.  The structures of RCs from the purple bacterial species Rhodopseudomonas viridis and Rhodobacter sphaeroides have been solved by X-ray crystallography [1-8].  Figure 1 shows the Rb. sphaeroides structure as described by Ermler et al. [6].  The complex contains four molecules of bacteriochlorophyll (BChl), two molecules of bacteriopheophytin (BPh), two quinones and an iron atom, all bound to three polypeptides.  Two of the BChls form a dimer that is often called the “special pair” (P).  The other BChls (BL and BM), the BPhs (HL and HM), and the quinones (QA and QB) extend from P in two branches on either side of an axis of approximate symmetry.  A 180˚ rotation about this axis interchanges the corresponding pigments on the two branches, along with the corresponding amino acid residues of the L and M subunits.  The L and M subunits have very similar structures, and many of the corresponding residues either are identical or involve conservative replacements.  However, a carotenoid (car) that plays mainly a protective role is located asymmetrically near BM.

When RCs are excited with light, the excitation energy moves to P within about 100 fs.  The excited dimer (P*) then transfers an electron to one of the BPhs (HL) with a time constant of about 3 ps [9-17].  An electron moves from the reduced BPh () to one of the quinones (QA) in about 200 ps [9,18,19].  These reactions proceed with a quantum yield (molar ratio of products formed to photons absorbed) of essentially 100% [20].  They also have the unusual property of speeding up with decreasing temperature: they are faster at 4K than at room temperature [10,15,21-25].  In addition, the initial steps are surprisingly specific: in spite of the approximate rotational symmetry of the RC, electron transfer from P* to HL is several orders of magnitude faster than transfer to HM [26-28].

Reaction centers provide ideal systems for exploring relationships between protein structure and function.  First, they carry out a variety of energy- and electron-transfer reactions ranging in time scale from 10-14 to 102 s.  Because these reactions can be started with precise timing by a short flash of light, their kinetics can be measured over a broad range of temperatures or under other conditions such as in the presence of an oriented electric or magnetic field, and the electron carriers provide spectroscopic signatures that lend themselves to such measurements.  The protein structures are known to high resolution and can be modified easily by site-directed mutagenesis.  In addition, the initial reactions occur on the short time scales that are accessible to microscopic (all-atom) computer simulations.  Although electron-transfer reactions between bound groups in proteins involve relatively simple chemistry, the factors that control their speed, specificity and temperature dependence are fundamentally the same as those that control other enzymatic processes.  The following sections describe some of the recent experimental and computational studies of the initial electron-transfer steps in bacterial RCs, with an emphasis on work in our lab.

 

The Initial Steps of Charge Separation

 

Because bacteriochlorophyll BL is situated between P and HL (see Fig. 1), it seems reasonable to suggest that an electron first jumps from P* to BL to form a  radical-pair.  Transfer of an electron from  to HL then would form :

 

                                                                       

 

However, this scheme assumes that the energies of P*, and  decrease in the same order: .  The movement of an electron from P* to HL must not involve any steps that are significantly uphill in energy because it occurs rapidly at 4 K.  Another possibility is that  is not formed as a real intermediate, but simply acts to couple P* and  by mixing with them quantum mechanically.  This could work even if  lies above P* in energy, as long as the energy gap is not too large and the orbital overlap of P, BL and HL is sufficiently strong.  Electronic coupling of this nature is termed superexchange. 

Initial attempts to detect  after excitation of RCs with sub-picosecond flashes were unsuccesful, and thus favored the superexchange mechanism.  Subsequent studies, however, have revealed transient absorbance changes that support the two-step mechanism with  as an intermediate [13,29-31].  Holzapfel et al. [13] assign a time constant of ~3 ps to the first step (P* ® ) at 295 K, and a time constant of ~0.9 ps to the second ( ® ).  Holzwarth and Muller [29] have suggested that both steps are reversible and have time constants of about 1.5 ps.  However,  remains elusive and some investigators still find the experimental evidence for the two-step mechanism not entirely convincing.

As mentioned above, the distinction between superexchange and the two-step mechanism hinges largely on the energy of .  If  lies above P* the reaction probably occurs by superexchange; if it is below P*, then  probably is a real intermediate.  The energies of these states also could bear on the specificity of the reaction: electron transfer to BL and HL would be favored if  lies below P* while  is significantly higher in energy.  Because experimental measurements of  and  are problematic, we have explored ways of calculating the energies of these states directly from the crystal structure [32-44].  Such calculations require evaluating the electrostatic interactions of the electron carriers with each other and with the protein, solvent and membrane, taking dielectric screening into account as realistically as possible.  They also require evaluating the molecular-orbital, or “gas-phase” energy differences between the ion-pair states and P* (Da12).  We calculated the electrostatic energies by the protein-dipoles-Langevin-dipoles (PDLD) method, in which dielectric effects are represented explicitly by induced dipoles in the protein and the surroundings.  We also have used molecular-dynamics (MD) simulations with free-energy-perturbation (FEP) methods.  (See the papers cited above for details.)  To circumvent quantum mechanical calculations of the gas-phase energy Da12, we combined calculated solvation energies with experimental information on the free energy of  and on the reduction potentials of BChl and BPh in solution.  The calculations placed  2 to 3 kcal/mol below P* in energy, in a good position to serve as a real intermediate.  However, the estimated uncertainty of ±3 kcal/mol left open the possibility that  was slightly above P*, so that the reaction might have to depend partly on superexchange.

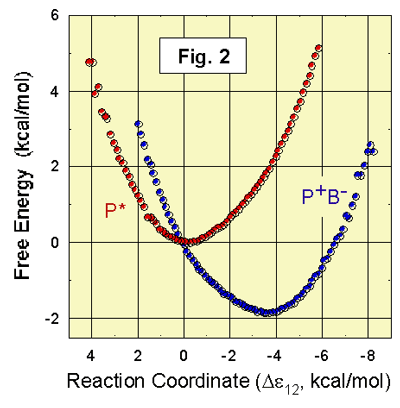
Figure 2 shows the results of recent calculations of the free-energies of P*BL and in Rb. sphaeroides RCs.  These calculations were done by running separate, 1-ns MD trajectories in the reactant and states.  The trajectories were propagated in steps of 1 fs, and the energy difference between  and P*BL (De12) was calculated every 10 fs.  The energy gap De12 provides a convenient way of representing the reaction coordinate because transitions between the two states can occur only when the energy difference is close to zero.  In a classical treatment, De12 must be 0 in order for the transition to conserve energy and momentum.  The requirements are less restrictive in a quantum mechanical treatment that considers nuclear tunneling, but the probability of making a transition still peaks sharply at De12 = 0.

If the fluctuating, time-dependent energy gap is calculated over a sufficiently long trajectory, the relative free energies of  and P*BL can be defined as a function of the reaction coordinate by writing

 

                                       .                                       (1)

 

Here Dgi(x) is the free energy of state i, Pi(x) is the average probability of finding an energy difference De12 = x at any given time during a trajectory in state i, kB is the Boltzmann constant, T is the temperature, and  is a constant that relates to the standard free energy difference between  and P*BL ().  The probability functions obtained from trajectories in both states can be combined with appropriate weighting factors in order to improve the sampling of the configurational space.  In Fig. 2, free energies are expressed relative to the minimum free energy of P*BL.  The gas-phase energy difference Da12 was adjusted arbitrarily so that De12 = 0 at this point.  The additive constant  was calculated by an FEP procedure in which the system was converted from P*BL to  in 10 steps and then returned to P*BL in another 10 steps; the forward and reverse calculations gave essentially the same result (-1.9 kcal/mol for P*BL ® ), as did the theoretical “linear response” expression for the standard free energy change:  where  and  are the mean values of the energy gap during trajectories in the two states.

The kinetics of many electron-transfer reactions can be described well by the semiclassical Marcus equation [45,46]:

 

                        .                    (2)

 

In this expression, k12 is the rate constant, s12 is an electronic coupling factor,  again is the standard free energy change, and l is the reorganization energy.  The reorganization energy is the energy required to move a system in state 1 along the reaction coordinate from the most-probable configuration of state 1 to the most-probable configuration of state 2.  (This usually is about the same as the energy needed to move move a system in state 2 from its most-probable configuration to the most-probable configuration of state 1.)  According to the Marcus equation, the activation free energy (DG‡) for an electron-transfer reaction is

 

                                                .                                               (3)

 

If   » -l, the free energy curves of the reactant and product intersect near the minimum of the reactant curve.  The activation free energy then is zero and, from eq. 2, the rate constant should increase slightly with decreasing temperature.

In the simulations shown in Fig. 2, the calculated  for P* ®  is about –1.9 kcal/mol and the protein reorganization energy (l) is about 1.8 kcal/mol.  The resulting activation energy is essentially zero.  These calculations do not include the internal reorganization energies of P and BL, which would increase l slightly but would leave DG‡ still very small.  Other simulations have given similar reorganization energies on the order of 1 to 2 kcal/mol for P* ®  and 4 to 5 kcal/mol for P* ®  [32,47].  These values are considerably smaller than typical solvent reorganization energies for electron-transfer reactions in solution.  For example, intramolecular electron-transfer to the heme from Ru derivatives attached near the surface of cytochrome-c involves reorganization energies in the range of 15 to 30 kcal/mol [48].  The small reorganization energy in the RC probably reflects the fact that the photosynthetic electron carriers are buried in the hydrophobic core of an integral membrane protein, which in turn is surrounded by phospholipids or in the case of purified RCs by a belt of detergents.  In addition, delocalization of the charges of P+, BL- and HL- over large p-electron systems makes the fields acting on the surrounding amino acid residues relatively weak.  The combination of small reorganization energies and small energy gaps with DGo » -l is consistent with the fast, and nearly temperature-independent kinetics of charge separation.

Experimental estimates of the free energy of  eventually were obtained by measuring the population of  in equilibrium with P+Phe- in RCs that contained Phe instead of HL, and using the known difference between the reduction potentials of Phe and BPh in solution [30,49,50].   was found to be about 1 kcal/mol below P*, in reasonably good agreement with the computational results described above.  A similar estimate was obtained from the effects of replacing BChl BL by BPh [51].

Since  appears to be slightly below P*BL in energy, the two-step sequence P* ®  ®  probably is the dominant pathway of charge separation in purple bacterial RCs.  Although quantum effects that are not included in the Marcus equation need to be considered at low temperatures and can be particularly important if ‑ >> l [36], they probably have little effect on the overall mechanism of the reaction at room temperature.   Alternative pathways may come into play if BL or HL is excited instead of P [52-54].

The calculated energy gap De12(t) between P* and  fluctuates over a range of about 5 kcal/mol on sub-picosecond time scales.  Because the mean energy gap  probably is less than 2 kcal/mol, these fluctuations cause De12(t) to pass back and forth through zero frequently on the picosecond time scale.  As mentioned above, each such crossing provides an opportunity for an electron to jump from P* to BL.  The fluctuations De12(t) through zero can account for the measured kinetics of charge separation if the electronic coupling factor s12 is on the order of 20 cm-1, which is close to the value predicted on the basis of the crystal structure and semiempirical molecular orbital theory.

Similar calculations put  5 to 6 kcal/mol above P* in free energy, giving the formation of this state a large activation free energy.  The energy difference between   and  seems sufficient to account for the specificity of the charge-separation pathway in favor of .

Before such microscopic computer simulations of complex systems were possible, the parameters s12 and l were obtained for many systems by fitting the Marcus equation to experimental data on the rate constant as functions of  or temperature.  In many cases, however, it is difficult to change  over a wide range experimentally without affecting the parameters of interest.  Increasingly reliable techniques for calculating properties such as s12, l, DG‡ and  directly from protein crystal structures are opening up new ways to explore how proteins adjust these parameters and thus control the rates of enzymatic reactions.  Additional discussion of these techniques and examples of applications to other systems can be found in reference 44.

 

Effects of Mutations on the Electron-Transfer Kinetics and Specificity

 

The effects of changing the free energy of  can be studied by mutating amino acid residues near the pigments.  Tyrosine 210 in the M polypeptide (Y(M210)), for example, is located close to both P and BL and probably is oriented so that the dipole of its phenolic OH group stabilizes  [33,55].  Replacing Y(M210) by Phe, Trp or Ile would be expected to raise the free energy of .  In accord with this expectation, these mutations slow charge separation and make it thermally activated [23,56-63].  Instead of speeding up with decreasing temperature, the reaction now slows down.  The increase in the activation energy in the Y(M210)W mutant is on the order of 0.8 kcal/mol [23].  Calculations of the free energy surfaces for P* and  in Rps. viridis reaction centers gave a similar increase in the calculated free energy of activation [64].

Mutations of residues that form hydrogen bonds to the BChls of P also affect the charge-separation dynamics [15,65-69].  In wild-type RCs from Rb. sphaeroides, for example, the acetyl group of one of the BChls of P forms an H-bond to H(L)168.  Removing this bond lowers the midpoint reduction potential (Em) of P, and thus should stabilize ; adding an H-bond to the acetyl of the other BChl or to the keto group of either BChl raises the Em, which should destabilize .  Mutations that should increase the energy of  are found to slow electron transfer, while mutations that should stabilize  speed it up.

In addition to affecting the rate of electron transfer, mutations of Y(M210) and the homologous residue in the L polypeptide (F(L181)) alter the specificity of charge separation.  In recent work, Kirmaier et al. [70] obtained about 30% “wrong way” electron transfer to HM by combining the double mutation Y(M210)F/F(L181)Y with an additional mutation that, by itself, had little effect on the specificity but facilitated the experimental resolution of  from .  This finding supports the view that the directionality of the charge-separation process hinges largely on the relative energies of  and .  However, a difference between the electronic coupling of P* to these two states also could be important [71-73].

  Low-frequency structural fluctuations of polar groups like the phenolic OH group of tyrosine M210 could explain the additional experimental observation that the electron-transfer kinetics are multiphasic.  Although the OH group of tyrosine M210 probably spends most of the time in an orientation that stabilizes , it may have a small probability of pointing in the opposite direction [55].  Reaction centers that happen to be in configurations with a large value of De12 at the time of an excitation flash must evolve into a more favorable configuration before they can react.

In recent work, we found that mutations of Arg (L135) or (M164) to Leu or Glu caused small shifts of the Em and absorption spectrum of P, but had very little effect on the charge-separation kinetics [74].  These residues occupy homologous positions on either side of the RC, with their ionizable groups about 14.5 Å from the center of P.  Their electrostatic interactions with P clearly are very strongly screened.  Although the ionizable groups of the Arg residues are almost completely buried in the protein, this screening could result largely from counterions in the nearby solvent, which keep the net charge of the system effectively constant.  We have used the effects of these and other mutations on the Em of P to test computational methods for treating dielectric screening in proteins.

 

Vibrational Modes, Wavepackets and Relaxations

 

The initial electron-transfer steps from P* to  occur too rapidly for the vibrational levels of the electron carriers to remain in thermal equilibrium with the surroundings.  Evidence for this is seen in oscillations in the fluorescence emission and excited-state absorption spectra following excitation of RCs with sub-picosecond flashes [15,75-84].  The oscillations can be described in terms of a vibrational wavepacket in the excited state.  A vibrational wavepacket consists of a coherent combination of vibrational wavefunctions for multiple levels of a particular vibrational mode.  A supicosecond flash can excite RCs into many different vibrational levels, creating such a wavepacket, because it intrinsically covers a broad spectrum of energies.  As long as the vibrational wavefunctions retain their originial phases, the wavepacket behaves much like a classical particle whose probability density moves back and forth with time along the vibrational coordinate.  These movements cause the emission and absorption spectra to oscillate at the frequency of the vibrational mode.  In mutants in which the lifetime of P* is extended, the damping of the oscillations provides a measure of the time required for the loss of vibrational coherence, which can occur as a result of thermal equilibration with the surroundings or through random fluctuations of the vibrational energies.  The damping occurs on the time scale of 1 to 2 ps, depending to some extent on the vibrational frequency [77]. 

Some of the oscillations seen after excitation of reaction centers with short flashes could reflect oscillations in the formation of  or  [79-82,84].  Vos et al. [82] have described an oscillation of the 800-nm absorption band of BL and BM, which they attribute to an electrochromic (Stark) effect of electric fields from .  This oscillation, which has an energy of about 30 cm-1 in wild-type reaction centers, is not seen in a mutant where the initial charge-separation reaction is greatly slowed.  Its phase varies across the absorption band in the manner expected if the formation of  occurs partly in a stepwise manner.  Increases in the amount of  presumably occur at times when a vibrational wavepacket in  intersects the potential energy surface of  .  Shuvalov and coworkers [81,84] have described similar oscillations in an absorption band at 1020 nm, which they assign to .  However, Spörlein et al. [83] have argued that the oscillations in the light-induced signals in this region are explained well by the oscillating spectrum of stimulated emission from P*, and probably do not reflect stepwise electron transfer.

Yakovlev et al. [81] suggest that P* and  mix strongly each time a P* wavepacket  crosses the potential surface of , so that the population of  increases abruptly at these points, but that the system remains in  only if it relaxes before the wavepacket moves away from the intersection.  Yakovlev et al. reason that a wavepacket moving on the 130-cm-1 vibrational coordinate could pass through the crossing region too rapidly for  to relax, so that the system usually returns to P*.  (An energy of 130 cm-1 corresponds to a vibrational period of 0.25 ps.)   The slower motion on the 30-cm-1 coordinate could couple more efficiently to charge separation because it allows more time for  to relax.  Several other authors have suggested similar pictures in which the overall rate of electron transfer is limited by vibrational relaxations that pull  out of resonance with P*BL [85,86].

How rapidly would  be expected to relax?  One way to address this question is to calculate the autocorrelation function of the energy gap between the two states [37,38,44,87-89].  The autocorrelation function is

 

                                         ,                                                 (4)

 

where the u(t) are the fluctuations of the energy gap about its mean value (u(t) = De12(t) - ).  From statistical mechanical principles, the decay time course of the autocorrelation function should be the same as the average relaxation of the product.  Figure 3 shows an autocorrelation function of the energy gap between  P* and  as calculated from a 1-ns trajectory  of Rb. sphaeroides reaction centers.  The insert shows the same function over a longer period of time.  Ai(t) is normalized to 0 at zero time in both plots.  The autocorrelation function decays most of the way to zero with a time constant between 50 and 100 fs (1 fs = 10-15 s), although small oscillatory components persist for several ps.  The relaxation of De12(t) in  or  also can be calculated directly by averaging the time-dependent energy gaps over many trajectories beginning at transitions to the product states, and such an average exhibits essentially identical kinetics.  The time scale of the relaxation seems qualitatively consistent with the picture suggested by Yakovlev et al. [81].

The frequencies of the vibrational modes that are coupled strongly to electron transfer can be extracted by taking a Fourier transform of the autocorrelation function A(t).  Such a transform gives the power spectrum of the fluctuations of De12(t).  A particular mode will contribute to the fluctuations of De12(t) if the vibrational potential energy function is shifted along the vibrational coordinate in  relative to P*.  Each such vibrational mode appears as a peak in the Fourier transform of A(t), and (assuming that the vibrational frequency is the same in  and P*) the amplitude of the peak is proportional to the magnitude of the shift.  Modes that do not shift or change in frequency do not contribute to the fluctuations of De12(t) and have no direct influence on the rate of electron transfer.

The power spectrum of De12(t) for P* ®  reveals a quasicontinuum of vibrational modes with 10 to 20 resolvable peaks between 10 and 400 cm-1 [43,87,90].  Figure 4 shows a typical spectrum for reaction centers of Rb. sphaeroides.  The peaks near 300 and between 355 and 385 cm-1 involve the O-H dipole of tyrosine (M)210 (peaks at the same positions dominate the Fourier transform of the autocorrelation function of the tyrosine CE2-CZ-OH-HOH dihedral angle).  Oscillations of the homologous tyrosine (M)208 were seen at somewhat lower frequencies in Rps. viridis [55].  The peaks in the regions of 30 and 130 cm-1 could reflect the oscillations with these energies that are seen in the absorption and emission spectra when reaction centers are excited with subpicosecond flashes.  These have not yet been assigned to particular motions, although some of the modes in the 130-cm-1 region could involve the acetyl groups of the BChls of P [91].  Low-frequency oscillations of the distance between P and BL also could be important [43].

 




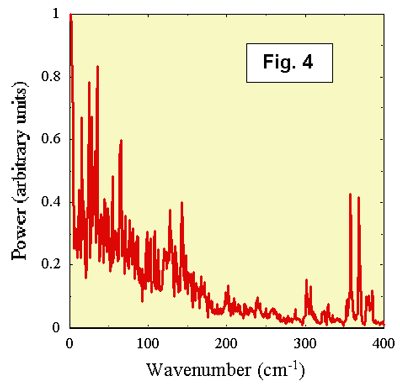References

1.     Deisenhofer J, Epp O, Miki K, Huber R & Michel H (1985) Structure of the protein subunits in the photosynthetic reaction centre of Rhodopseudomonas viridis at 3 Å resolution. Nature 318: 618-624.

2.     Deisenhofer J, Epp O, Sinning I & Michel H (1995) Crystallographic refinement at 2.3 Å resolution and refined model of the photosynthetic reaction centre from Rhodopseudomonas viridis. J. Mol. Biol. 246: 429-457.

3.     Allen JP, Feher G, Yeates TO, Komiya H & Rees DC (1987) Structure of the reaction center from Rhodobacter sphaeroides R-26: the protein subunits. Proc. Natl. Acad. Sci. USA 84: 6162-6166.

4.     Allen JP, Feher G, Yeates TO, Komiya H & Rees DC (1987) Structure of the reaction center from Rhodobacter sphaeroides R-26: the cofactors. Proc. Natl. Acad. Sci. USA 84: 5730-5734.

5.     Chang CH, El-Kabbani O, Tiede D, Norris J & Schiffer M (1991) Structure of the membrane-bound protein photosynthetic reaction center from Rhodobacter sphaeroides. Biochem. 30: 5352-5360.

6.     Ermler U, Fritzsch G, Buchanan SK & Michel H (1994) Structure of the photosynthetic reaction centre from Rhodobacter sphaeroides at 2.65 Å resolution: cofactors and protein-cofacter interactions. Structure 2:  925-936.

7.     McAuley KE, Fyfe PK, Ridge JP, cogdell RJ, Isaacs NW et al. (2000) Ubiquinone binding, ubiquinone exclusion, and detailed cofactor conformation in a mutant bacterial reaction center. Biochem. 39: 15032-15043.

8.     Fyfe PK & Jones MR (2000) Re-emerging structures: continuing crystallography of the bacterial reaction centre. Biochim. Biophys. Acta Bioenerg. 1459: 413-421.

9.     Holten D, Windsor MW, Parson WW & Thornber JP (1978) Primary photochemical processes in isolated reaction centers of Rhodopseudomonas viridis. Biochim. Biophys Acta 501: 112-126.

10.   Woodbury NW, Becker M, Middendorf D & Parson WW (1985) Picosecond kinetics of the initial photochemical electron-transfer reaction in bacterial photosynthetic reaction center. Biochem. 24: 7516-7521.

11.   Breton J, Martin J-L, Migus A, Antonetti A & Orszag A (1986) Femtosecond spectroscopy of excitation electron transfer and initial charge separation in the reaction center of the photosynthetic bacterium Rhodopseudomonas viridis. Proc. Natl. Acad. Sci. USA 83: 5121-5175.

12.   Holzapfel W, Finkele U, Kaiser W, Oesterhelt D, Scheer H et al. (1989) Observation of a bacteriochlorophyll anion radical during the primary charge separation in a reaction center. Chem. Phys. Lett. 160: 1-7.

13.   Holzapfel W, Finkele U, Kaiser W, Oesterhelt D, Scheer H et al. (1990) Initial electron transfer in the reaction center from Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA 87: 5168-5172.

14.   Kirmaier C & Holten D (1988) Subpicosecond spectroscopy of charge separation in Rhodobacter capsulatus reaction centers. Israel J. Chem. 28: 79-85.

15.   Woodbury NW, Peloquin JM, Alden RG, X. L, Taguchi AKW et al. (1994) Relationship between thermodynamics and mechanism during photoinduced charge separation in reaction centers from Rhodobacter sphaeroides. Biochem. 33: 8101-8112.

16.   Martin J-L, Breton J, Hoff AJ, Migus A & Antonetti A (1986) Femtosecond spectroscopy of electron transfer in the reaction center of the photosynthetic bacterium Rhodopseudomonas sphaeroides R-26:  direct electron transfer from the dimeric bacteriochlorophyll primary donor to the bacteriopheophytin acceptor with a time constant of 2.8 ± 0.2 psec. Proc. Natl. Acad. Sci. USA 83: 957-961.

17.   Paschenko VZ, Korvatovskii BN, Kononenko AA, Chamorovsky SK & Rubin AB (1985) Estimation of the rate of photchemical charge separation in Rhodopseudomonas spheroides reaction centers by fluorescence and absorption picosecond spectroscopy. FEBS Lett. 191: 245-248.

18.   Kaufmann KJ, Petty KM, Dutton PL & Rentzepis PM (1975) Picosecond kinetics of events leading to reaction center bacteriochlorophyll oxidation. Science 188: 1301-1304.

19.   Rockley MG, Windsor MW, Cogdell RJ & Parson WW (1975) Picosecond detection of an intermediate in the photochemical reaction of bacterial photosynthesis. Proc. Natl. Acad. Sci. USA 72: 2251-2255.

20.   Wraight CA & Clayton RK (1973) The absolute quantum efficiency of bacteriochlorophyll photooxidation in reaction centres of Rhodopseudomonas spheroides. Biochim. Biophys Acta 333: 246-260.

21.   Breton J, Martin J-L, Fleming GR & Lambry J-C (1988) Low temperature femtosecond spectroscopy of the initial step of electron transfer in reaction centers from photosynthetic purple bacteria. Biochem. 27: 8276-8284.

22.   Fleming GR, Martin J-L & Breton J (1988) Rates of primary electron transfer in photosynthetic reaction centers and their mechanistic implications. Nature 33: 190-192.

23.   Nagarajan V, Parson WW, Davis D & Schenck CC (1993) Kinetics and free energy gaps of electron-transfer reactions in Rhodobacter sphaeroides reaction centers. Biochem. 32: 12324-12336.

24.   Kirmaier C, Holten D & Parson WW (1985) Temperature and detection-wavelength dependence of the picosecond electron-transfer kinetics measured in Rhodopseudomonas sphaeroides reaction centers.  Resolution of new spectral and kinetic components in the primary charge-separation process. Biochim. Biophys. Acta 810: 33-48.

25.   Lauterwasser C, Finkele U, Scheer. H & Zinth W (1991) Temperature dependence of the primary electron transfer in photosynthetic reaction centers from Rhodobacter sphaeroides. Chem. Phys. Lett. 183: 471-477.

26.   Kirmaier C, Holten D & Parson WW (1985) Picosecond photodichroism studies of the transient states in Rhodopseudomonas sphaeroides reaction centers at 5 K: effects of electron transfer on the six bacteriochlorin pigments. Biochim. Biophys. Acta 810: 49-61.

27.   Bylina EJ, Kirmaier C, McDowell L, Holten D & Youvan DC (1988) Influence of an amino-acid residue on the optical properties and electron transfer dynamics of a photosynthetic reaction centre complex. Nature 336: 182-184.

28.   Kellog EC, Kolaczkowski S, Wasielewski MR & Tiede DM (1989) Measurement of the extent of electron transfer to the bacteriopheophytin in the M-subunit in reaction centers of Rhodopseudomonas viridis. Photosynth. Res. 22: 47-59.

29.   Holzwarth AR & Muller MG (1996) Energetics and kinetics of radical pairs in reaction centers from Rhodobacter sphaeroides.  A femtosecond transient absorption study. Biochem. 35: 11820-11831.

30.   Kennis JTM, Shkuropatov AY, van Stokkum IHM, Gast P, Hoff AJ et al. (1997) Formation of a long-lived P+BA- state in plant pheophytin-exchanged reaction centers of Rhodobacter sphaeroides R26 at low temperature. Biochem. 36: 16231-16238.

31.   van Stokkum IHM, Beekman LMP, Jones MR, van Brederode ME & van Grondelle R (1997) Primary electron transfer kinetics in membrane-bound Rhodobacter sphaeroides reaction centers: a global and target analysis. Biochem. 36: 11360-11368.

32.   Creighton S, Hwang J-K, Warshel A, Parson WW & Norris J (1988) Simulating the dynamics of the primary charge separation process in bacterial photosynthesis. Biochem. 27: 774-781.

33.   Parson WW, Chu ZT & Warshel A (1990) Electrostatic control of charge separation in bacterial photosynthesis. Biochim. Biophys. Acta 1017: 251-272.

34.   Alden RG, Parson WW, Chu ZT & Warshel A (1995) Calculations of electrostatic energies in photosynthetic reaction centers. J. Am. Chem. Soc. 117: 12284-12298.

35.   Alden RG, Parson WW, Chu ZT & Warshel A, Macroscopic and microscopic estimates of the energetics of charge separation in bacterial reaction centers, in Reaction Centers of Photosynthetic Bacteria:  Structure and Dynamics, Michel-Beyerle, ME, Editor. 1996, Springer-Verlag: Berlin. 105-116.

36.   Warshel A, Chu ZT & Parson WW (1989) Dispersed polaron simulations of electron transfer in photosynthetic reaction centers. Science 246: 112-116.

37.   Warshel A & Parson WW (1991) Computer simulations of electron transfer reactions in solution and photosynthetic reaction centers. Ann. Rev. Phys. Chem. 42: 279-309.

38.   Parson WW & Warshel A, Simulations of electron transfer in bacterial reaction centers, in The Photosynthetic Reaction Center, Norris, J and Deisenhofer, J, Editors. 1993, Academic Press: San Diego. 23-47.

39.   Parson WW & Warshel A, Theoretical analyses of electron-transfer reactions, in Anoxygenic Photosynthetic Bacteria, Blankenship, RE, Madigan, MT, and Bauer, CE, Editors. 1994, Academic Publishers. 559-575.

40.   Warshel A, Chu ZT & Parson WW (1994) On the energetics of the primary electron-transfer process in bacterial reaction centers. J. Photochem. Photobiol. A: Chem. 82: 123-128.

41.   Warshel A, Chu ZT & Parson WW (1997) Two-dimensional free energy surfaces for primary electron transfer in a photosynthetic reaction center. Chem. Phys. Lett. 265: 293-296.

42.   Parson WW, Chu ZT & Warshel A (1998) Reorganization energy of the initial electron-transfer step in photosynthetic bacterial reaction centers. Biophys. J. 74: 182-191.

43.   Parson WW, Chu ZT & Warshel A (1997) Oscillations of the energy gap for the initial electron-transfer step in bacterial reaction centers. Photosyn. Res. 55: 147-152.

44.   Warshel A & Parson WW (2001) Dynamics of biochemical and biophysical reactions: insight from computer simulations. Quart. Rev. Biophys. 34: 563-679.

45.   Marcus RA (1956) On the theory of oxidation-reduction reactions involving electron-transfer. I. J. Chem. Phys. 24: 966-978.

46.   Marcus RA & Sutin N (1985) Electron transfers in chemistry and biology. Biochem. Biophys. Acta 811: 265-322.

47.   Parson WW, Chu ZT & Warshel A, Free energy functions for charge separation in wild-type and mutant bacterial reaction centers, in Photosynthesis: Mechanisms and Effects, Garab, G, Editor. 1998, Kluwer Acad. Publ.: Dordecht. 703-706.

48.   Meade TJ, Gray HB & Winkler JR (1989) Driving-force effects on the rate of long-range electron transfer in ruthenium-modified cytochrome-c. J. Am. Chem. Soc. 111: 4353-4356.

49.   Schmidt S, Arlt  T, Hamm P, Huber H, Nägele T et al. (1995) Primary electron-transfer dynamics in modified bacterial reaction centers containing pheophytin-a instead of bacteriopheophytin-a. Spectrochim. Acta A 51A: 1565-1578.

50.   Shkuropatov AY & Shuvalov VA (1993) Electron transfer in pheophytin a-modified reaction centers from Rhodobacter sphaeroides (R-26). FEBS. Lett. 322: 168-172.

51.   Arlt T, Dohse B, Schmidt S, Wachtveitl J, Laussermaier E et al. (1996) Electron transfer dynamics of Rhodopseudomonas viridis reaction centers with a modified binding site for the accessory bacteriochlorophyll. Biochem. 35: 9235-9244.

52.   Lin S, Taguchi AKW & Woodbury NW (1996) Excitation wavelength dependence of energy transfer and charge separation in reaction centers from Rhodobacter sphaeroides: Evidence for adiabatic electron transfer. J. Phys. Chem. 100: 17067-17078.

53.   van Brederode ME, Jones MR, van Mourik F, van Stokkum IHM & van Grondelle R (1997) A new pathway for transmembrane electron transfer in photosynthetic reaction centers of Rhodobacter sphaeroides not involving the excited special pair. Biochem. 36: 6855-6861.

54.   van Brederode ME, van Mourik F, van Stokkum IHM, Jones MR & van Grondelle R (1999) Multiple pathways for ultrafast transduction of light energy in the photosynthetic reaction center of Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA 96: 2054-2059.

55.   Alden RG, Parson WW, Chu ZT & Warshel A (1996) Orientation of the OH dipole of tyrosine (M)210 and its effect on electrostatic energies in photosynthetic bacterial reaction centers. J. Phys. Chem. 100: 16761-16770.

56.   Parson WW, Nagarajan V, Gaul D, Schenck CC, Chu ZT et al., Electrostatic effects on the speed and directionality of electron transfer in bacterial reaction centers: the special role of tyrosine M-208, in Reaction Centers of Photosynthetic Bacteria, Michel-Beyerle, M-E, Editor. 1990, Springer-Verlag: Berlin. 239-249.

57.   Chan CK, Chen LXQ, Dimagno TJ, Hanson DK, Nance SL et al. (1991) Mechanism of the initial charge separation in photosynthetic bacterial reaction centers. Chem. Phys. Lett. 176: 366-372.

58.   Finkele U, Lauterwasser C, Zinth W, Gray KA & Oesterhelt D (1990) Role of tyrosine M210 in the initial charge separation of reaction centers of Rhodobacter sphaeroides. Biochem. 29: 8517-8521.

59.   Gray KA, Wachtveitl J & Oesterhelt D (1992) Photochemical trapping of a bacteriopheophytin anion in site-specific reaction-center mutants from the photosynthetic bacterium Rhodobacter sphaeroides. Eur. J. Biochem. 207: 723-731.

60.   Nagarajan V, Parson WW, Gaul D & Schenck C (1990) Effect of directed mutations of the tyrosine at site (M)210 on the primary photosynthetic electron transfer process in Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA 87: 7888-7892.

61.   Jia Y, DiMagno TJ, Chan C-K, Wang Z, Du M et al. (1993) Primary charge separation in mutant reaction centers of Rhodobacter capsulatus. J. Phys. Chem. 97: 13180-13191.

62.   Shochat S, Arlt T, Francke C, Gast P, van Noort PI et al. (1994) Spectroscopic characterization of reaction centers of the (M)Y210W mutant of the photosynthetic bacterium Rhodobacter sphaeroides. Photosynth. Res. 40: 55-66.

63.   Beekman LMP, van Stokkum IHM, Monshouwer R, Rijnders AJ, McGlynn P et al. (1996) Primary electron transfer in membrane-bound reaction centers with mutations at the M210 position. J. Phys. Chem. 100: 7256-7268.

64.   Parson WW & Warshel A. Time-dependent free energy functions for charge separation in photosynthetic bacterial reaction centers. in Abstracts, 39th Sanibel Symposium. 1999. St. Augustine, FL.

65.   Williams JC, Alden RG, Murchison HA, Peloquin JM, Woodbury NW et al. (1992) Effects of mutations near the bacteriochlorophylls in reaction centers from Rhodobacter sphaeroides. Biochem. 31: 11029-11037.

66.   Allen JP, Williams JC, Graige MS, Paddock ML, Labahn A et al. (1998) Free energy dependence of the direct charge recombination from the primary and secondary quinones in reaction centers from Rhodobacter sphaeroides. Photosyn. Res. 55: 227-233.

67.   Lin X, Murchison HA, Nagarajan V, Parson WW, Allen JP et al. (1994) Specific alteration of the oxidation potential of the electron donor in reaction centers from Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA 91: 10265-10270.

68.   Mattioli TA, Williams JC, Allen JP & Robert B (1994) Changes in primary donor hydrogen bonding interactions in mutant reaction centers from Rhodobacter sphaeroides: Identification of the vibrational frequencies of all the conjugated carbonyl groups. Biochem. 33: 1636-1643.

69.   Arlt T, Bibikova M, Penzkofer H, Oesterhelt D & Zinth W (1996) Strong acceleration of primary photosynthetic electron transfer in a mutated reaction center of Rhodopseudomonas viridis. J. Phys. Chem. 100: 12060-12065.

70.   Kirmaier C, He C & Holten D (2001) Manipulating the direction of electron transfer in the bacterial reaction center by swapping Phe for Tyr near BChlM (L181) and Tyr for Phe near BChlL (M208). Biochem. 40: 12132-12139.

71.   Zhang LY & Friesner RA (1998) Ab initio calculation of electronic coupling in the photosynthetic reaction center. Proc. Natl. Acad. Sci. USA 95: 13603-13605.

72.   Ivashin N, Källenbring B, Larsson S & Hansson Ö (1998) Charge separation in photosynthetic reaction center. J. Phys. Chem. B. 102: 5017-5022.

73.   Kolbasov D & Scherz A (2000) Asymmetric electron transfer in reaction centers of purple bacteria strongly depends on different electron matrix elements in the active and inactive branches. J. Phys. Chem. B 104: 1802 -1809.

74.   Johnson E & Parson WW (2002) Electrostatic interactions in an integral membrane protein. Biochem. submitted.

75.   Vos MH, Rappaport F, Lambry J-H, Breton J & Martin J-L (1993) Visualization of coherent nuclear motion in a membrane protein by femtosecond spectroscopy. Nature 363: 320-325.

76.   Vos MH, Jones MR, Hunter CN, J. B & Martin J-L (1994) Coherent nuclear dynamics at room temperature in bacterial reaction centers. Proc. Natl. Acad. Sci. USA 91: 12701-12705.

77.   Vos MH, Jones MR, Breton J, Lambry JC & Martin J-L (1996) Vibrational dephasing of long- and short-lived primary donor excited states in mutant reaction centers of Rhodobacter sphaeroides. Biochem. 35: 2687-2692.

78.   Stanley RJ & Boxer SG (1995) Oscillations in spontaneous fluorescence from photosynthetic reaction centers. J. Phys. Chem. 99: 859-863.

79.   Streltsov AM, Aartsma TJ, Hoff AJ & Shuvalov VA (1997) Oscillations within the B-L absorption band of Rhodobacter sphaeroides reaction centers upon 30 femtosecond excitation at 865 nm. Chem. Phys. Letts. 266: 347-352.

80.   Streltsov AM, Vulto SIE, Shkuropatov AY, Hoff AJ, Aartsma TJ et al. (1998) BA and BB absorbance perturbations induced by coherent nuclear motions in reaction centers from Rhodobacter sphaeroides upon 30-fs excitation of the primary donor. J. Phys. Chem. B. 102: 7293-7298.

81.   Yakovlev AG, Shkuropatov AC & Shuvalov AV (2000) Nuclear wavepacket motion producing a reversible charge separation in bacterial reaction centers. FEBS Lett. 466: 209-212.

82.   Vos MH, Rischel C, Jones MR & Martin J-L (2000) Electrochromic detection of a coherent component in the formation of the charge pair P+HL- in bacterial reaction centers. Biochem. 39: 8353 -8361.

83.   Spörlein S, Zinth W & Wachtveitl J (1998) Vibrational coherence in photosynthetic reaction centers observed in the bacteriochlorophyll anion band. J. Phys. Chem. B 102: 7492-7496.

84.   Yakovlev AG & Shuvalov VA (2000) Formation of bacteriochlorophyll anion band at 1020 nm produced by nuclear wavepacket motion in bacterial reaction centers. J. Chin. Chem. Soc. 47: 1-6.

85.   Kitzing E & Kuhn H (1990) Primary electron transfer in photosynthetic reaction centers. J. Phys. Chem. 94: 1699-1702.

86.   Peloquin JM, Williams JC, Lin X, Alden RG, Taguchi AKW et al. (1994) Time-dependent thermodynamics during early electron transfer in reaction centers from Rhodobacter sphaeroides. Biochem. 33: 8089-8100.

87.   Schulten K & Tesch M (1991) Coupling of protein motion to electron transfer: molecular dynamics and stochastic quantum mechanics study of photosynthetic reaction centers. Chem. Phys. 158: 421-446.

88.   Treutlein H, Schulten K, Brunger AT, Karplus M, Deisenhofer J et al. (1992) Chromophore-protein interactions and the function of the photosynthetic reaction center: a molecular dynamics study. Proc. Natl. Acad. Sci. USA 89: 75-79.

89.   Marchi M, Gehlen JN, Chandler D & Newton M (1993) Diabatic surfaces and the pathway for primary electron transfer in a photosynthetic reaction center. J. Am. Chem. Soc. 115: 4178-4190.

90.   Souaille M & Marchi M (1997) Nuclear dynamics and electronic transition in a photosynthetic reaction center. J. Am. Chem. Soc. 119: 3948-3958.

91.   Czarnecki K, Chynwat V, Erickson JP, Frank HA & Bocian DF (1997) Characterization of the strongly coupled, low-frequency vibrational modes of the special pair of photosynthetic reaction centers via isotopic labeling of the cofactors. J. Am. Chem. Soc. 119: 415-426.