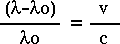
THE HUBBLE LAW	Measurements of Velocities and Distances

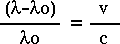
Step 3: Finding the velocity of each galaxy

The velocity is relatively easy for us to measure using the Doppler effect. An object in motion (in this case, being carried along by the expansion of space itself) will have its radiation (light) shifted in wavelength. For velocities much smaller than the speed of light, we can use the regular Doppler formula:

The quantity on the left side of this equation is usually called the redshift, and is denoted by the letter z.

The formula for redshift should remind you of the process where you calculated your percentage error: [(your value) - (true value)] / (true value). Thus, we can view the redshift (at least for those galaxies with a recessional velocity much less than the speed of light) as a "percentage" wavelength shift. It is a measure of the ratio between the velocity of the galaxy and the speed of light.

For this lab, all wavelengths will be measured in Ångstroms (Å), and we will approximate the speed of light at 300,000 km/sec. Thus, we can determine the velocity of a galaxy from its spectrum: we simply measure the (shifted) wavelength of a known absorption line and solve the equation v = z * c.

For Example: A certain absorption line that is found at 5000Å in the lab (rest wavelength) is found at 5050Å when analyzing the spectrum of a particular galaxy. We first calculate z:

redshift = [(measured wavelength) - (rest wavelength)] / (rest wavelength)

We find that z = 50/5000 = 0.001 and conclude that this galaxy is moving with a velocity v = 0.001 * c = 3000 km/sec away from us.

Measuring the Spectral Lines

The velocity of the galaxy is determined by measuring the redshift of spectral lines in the spectrum of the galaxy. The full optical (visual wavelengths) spectrum of the galaxy is shown at the top of the web page containing the spectrum of the galaxy being measured (see link below). Below it are enlarged portions of the same spectrum, in the vicinity of some common galaxy spectral features: the hydrogen transitions hydrogen-alpha (656.28 nm, 6562.8 Å), hydrogen-beta (486.13 nm, 4861.3 Å), hydrogen-delta (410.17 nm, 4101.7 Å) as well as the "K and H" lines of ionized calcium (393.37 and 396.85 nm, 3933.7 and 3968.5 Å). The enlarged portions of the same spectrum are "clickable" and will return a wavelength value corresponding to where you "clicked." Take a brief look at the spectrum for NGC1357 and the analysis of the spectrum. You should try to use similar logic when measuring the rest of your selected galaxies.
You are now ready to do your measurements.
1. Make sure you have a copy of the Data Table from the set of student answer sheets. (PDF)
2. Note that for each galaxy there are two lines of data under each "spectral lines" column. The first line contains the measured wavelength. The second line contains the calculated redshift.
3. Start with NGC 1357 to see if you can duplicate or come close to the values discussed under the analysis. Note how the data table has been filled in for NGC 1357, and make sure you understand what data goes where and what calculations are being done.
4. Move on to the next galaxy, NGC 1832. Note that this galaxy, too, has been measured for you. Again, see if your measurements mimic these data.
5. Use the velocities of these two galaxies as part of the 15 velocities needed to calculate the Hubble constant (leaving you only 13 to do!).
6. Now move on to the next galaxy that you have selected. Starting with the calcium lines, measure the wavelength of the same but shifted line by clicking at the middle of the spectral line (i.e. at the "greatest depth" of absorption or "peak" of emission)in the spectrum of the galaxy. Write this wavelength in the box below the appropriate line designation in your data table. (Note: It is due to the peculiarities of each galaxy that some spectral lines are absent, or show up in emission instead of absorption.)
7. Do this for the rest of your selected galaxies, trying to measure the shifts of at least 3 lines in the spectrum. For each of your galaxies, you will measure, calculate redshifts, average redshifts, derive a velocity (remember: v = z * c). These are the "y" values for your graph. Then you will be ready to find the "x" values -- the corresponding distances.
8. For the galaxies not used simply cross out the row next to the galaxy number.

Here is the listing of the files that contain the real data for the 27 galaxies.

Step 4: Finding the distance to each galaxy

A trickier task is to determine the distances to galaxies. For nearby galaxies, we can use standard candles such as Cepheid variables or Type I supernovae. But, for very distant galaxies, we must rely on more indirect methods. The key assumption for this lab is that galaxies of similar Hubble type are, in fact, of similar actual size, no matter how far away they are. This is known as "the standard ruler" assumption. We must first calibrate the actual size by using a galaxy to which we know the true distance. We are looking for galaxies in the sample that are Sb galaxies, as we would use the nearby Sb galaxy, M31 the Andromeda galaxy, to calibrate the distances. We know the distance to the Andromeda galaxy through observations of the Cepheid variables in it. Then, to determine the distance to more distant, similar galaxies, one would only need to measure their apparent (angular) sizes, and use the following approximation for small angles:

a = s / d
or:
d = s / a
where a is the measured angular size (in radians), s is the galaxy's true size (diameter), and d is the distance to the galaxy.

Measuring the Galaxies

It is up to you to decide the criteria you will use in measuring these galaxies. It is suggested that you try to measure as far out as you can see any fuzzy disk.
The angular size of the galaxy is measured by using its image. Note that the images used in this lab are negatives, so that bright objects -- such as stars and galaxies -- appear dark. Note also that there may be more than one galaxy in the image; the galaxy of interest is always the one closest to the center.
To measure the size, simply move the mouse and click on opposite ends of the galaxy, along its longest part. (You will need to make a total of two clicks.)
Take a look at this schematic of a galaxy viewed from three different angles. Thought question: We assume that the spirals are all round, and that their different shapes are simply because we are viewing them from different angles. When measuring the angular sizes of the galaxies, why should you measure along the longest axis only?
The angular size of the galaxy (in milliradians; 1 mrad = 0.057 degrees = 206 arcseconds) will be displayed; write this number down on your data table given in the student answer sheets, under "Galaxy Size."
If, at any point, you make an error while you're measuring (e.g. a mis-click), simply click on the "back" button of your web browser and take the measurement again.

Here is the listing of the files containing the real data for the 27 galaxies.

Checking Your Data

It would be a good idea to have your instructor look at your data now, before you do a ton of calculations. You wouldn't want to spend hours of your time only to discover that you made mistakes in steps 3 and 4.

Initial Calculations

If you feel confident of your data, then you are ready for the preliminary calculations:

Velocity Determination

For each measured line calculate the (redshift z), and enter this value in the box under the measured wavelength. Then take the average redshift of the measured lines for each galaxy, and enter it on the appropriate column. Finally, use this average redshift to calculate the velocity of the galaxy using the modified Doppler-shift formula:

v = c * z

Distance Determination

Determine the distance (in Mpc) to each galaxy using the following, revised version of the small angle formula. Recall, we have had to make an important assumption: all of these galaxies are about the same actual size. Once you have the angular diameter in mrad (and with some adjusting of units), just take the actual size of each galaxy -- 22 kpc -- and divide it by the measured angular diameter. For example, if one of the galaxies had a measured angular diameter of 0.50 mrad, 22 / 0.50 = 44 Mpc.

Details for the manipulation of the units to come out with the correct distances
From calibrations, we know that galaxies of the type used in this lab are about 22 kpc (1 kiloparsec = 1000 pc) across. We may then find the distance to the galaxies: distance (kpc) = size (kpc) / a (rad) or equivalently, upon multiplying the left side by 1000 and dividing the right side by 0.001 (which is exactly the same thing): distance (Mpc) = size (kpc) / a (mrad)
Note that we now have the equation in a form where we can simply substitute the size in kpc (22) and divide it by the angle returned by our measurements (already in mrad).

Go on to Steps 5 and 6

Last updated on:

THE HUBBLE LAW

Measurements of Velocities and Distances