PyClaw Geometry

The PyClaw geometry package contains the classes used to define the geometry of a Solution object. The base container for all other geometry is the Domain object. It contains a list of Patch objects that reside inside of the Domain.

Patch represents a piece of the domain that could be a different resolution than the others, have a different coordinate mapping, or be used to construct complex domain shapes.

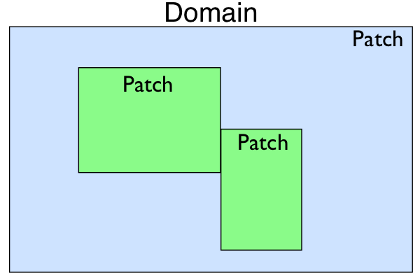
It contains Dimension objects that define the extent of the Patch and the number of grid cells in each dimension. Patch also contains a reference to a nearly identical Grid object. The Grid object also contains a set of Dimension objects describing its extent and number of grid cells. The Grid is meant to represent the geometry of the data local to the process in the case of a parallel run. In a serial simulation the Patch and Grid share the same dimensions.

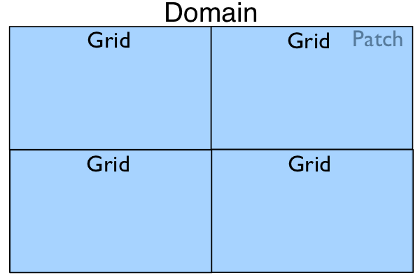
In the case where only one Patch object exists in a Domain but it is run with four processes in parallel, the Domain hierarchy could look like:

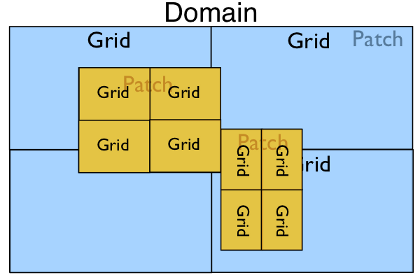
In the most complex case with multiple patches and a parallel run we may have the following:

Serial Geometry Objects

pyclaw.geometry.Domain

class clawpack.pyclaw.geometry.Domain(*arg)

A Domain is a list of Patches.

A Domain may be initialized in the following ways:

1. Using 3 arguments, which are in order

   • A list of the lower boundaries in each dimension

   • A list of the upper boundaries in each dimension

   • A list of the number of cells to be used in each dimension

2. Using a single argument, which is

   • A list of dimensions; or

   • A list of patches.

Examples

>>> from clawpack import pyclaw
>>> domain = pyclaw.Domain( (0.,0.), (1.,1.), (100,100))
>>> print(domain.num_dim)
2
>>> print(domain.grid.num_cells)
[100, 100]

property grid

(list) - Patch.grid of base patch

property num_dim

(int) - Patch.num_dim of base patch

property patch

(Patch) - First patch is returned

pyclaw.geometry.Patch

class clawpack.pyclaw.geometry.Patch(dimensions)

Bases: object

Global Patch information

Each patch has a value for level and patch_index.

add_dimension(dimension)

Add the specified dimension to this patch

Input

• dimension - (Dimension) Dimension to be added

get_dim_attribute(attr)

Returns a tuple of all dimensions’ attribute attr

property delta

(list) - List of computational cell widths

property dimensions

(list) - List of Dimension objects defining the grid’s extent and resolution

level = None

(int) - AMR level this patch belongs to, default = 1

property lower_global

(list) - Lower coordinate extents of each dimension

property name

(list) - List of names of each dimension

property num_cells_global

(list) - List of the number of cells in each dimension

property num_dim

(int) - Number of dimensions

patch_index = None

(int) - Patch number of current patch, default = 0

property upper_global

(list) - Upper coordinate extends of each dimension

pyclaw.geometry.Grid

class clawpack.pyclaw.geometry.Grid(dimensions)

Representation of a single grid.

Dimension information

Each dimension has an associated name with it that can be accessed via that name such as grid.x.num_cells which would access the x dimension’s number of cells.

Properties

If the requested property has multiple values, a list will be returned with the corresponding property belonging to the dimensions in order.

Initialization

Input:

• dimensions - (list of Dimension) Dimensions that are to be associated with this grid

Output:

• (grid) Initialized grid object

A PyClaw grid is usually constructed from a tuple of PyClaw Dimension objects:

>>> from clawpack.pyclaw.geometry import Dimension, Grid
>>> x = Dimension(0.,1.,10,name='x')
>>> y = Dimension(-1.,1.,25,name='y')
>>> grid = Grid((x,y))
>>> print(grid)
2-dimensional domain (x,y)
No mapping
Extent:  [0.0, 1.0] x [-1.0, 1.0]
Cells:  10 x 25

We can query various properties of the grid:

>>> grid.num_dim
2
>>> grid.num_cells
[10, 25]
>>> grid.lower
[0.0, -1.0]
>>> grid.delta # Returns [dx, dy]
[0.1, 0.08]

A grid can be extended to higher dimensions using the add_dimension() method:

>>> z=Dimension(-2.0,2.0,21,name='z')
>>> grid.add_dimension(z)
>>> grid.num_dim
3
>>> grid.num_cells
[10, 25, 21]

Coordinates:

We can get the x, y, and z-coordinate arrays of cell nodes and centers from the grid. Properties beginning with ‘c’ refer to the computational (unmapped) domain, while properties beginning with ‘p’ refer to the physical (mapped) domain. For grids with no mapping, the two are identical. Also note the difference between ‘center’ and ‘centers’.

>>> import numpy as np
>>> np.set_printoptions(precision=2)  # avoid doctest issues with roundoff
>>> grid.c_center([1,2,3])
array([ 0.15, -0.8 , -1.33])
>>> grid.p_nodes[0][0,0,0]
0.0
>>> grid.p_nodes[1][0,0,0]
-1.0
>>> grid.p_nodes[2][0,0,0]
-2.0

It’s also possible to get coordinates for ghost cell arrays:

>>> x = Dimension(0.,1.,5,name='x')
>>> grid1d = Grid([x])
>>> grid1d.c_centers
[array([0.1, 0.3, 0.5, 0.7, 0.9])]
>>> grid1d.c_centers_with_ghost(2)
[array([-0.3, -0.1,  0.1,  0.3,  0.5,  0.7,  0.9,  1.1,  1.3])]

Mappings:

A grid mapping can be used to solve in a domain that is not rectangular, or to adjust the local spacing of grid cells. For instance, we can use smaller cells on the left and larger cells on the right by doing:

>>> double = lambda xarr : np.array([x**2 for x in xarr])
>>> grid1d.mapc2p = double
>>> grid1d.p_centers
array([0.01, 0.09, 0.25, 0.49, 0.81])

Note that the ‘nodes’ (or nodes) of the mapped grid are the mapped values of the computational nodes. In general, they are not the midpoints between mapped centers:

>>> grid1d.p_nodes
array([0.  , 0.04, 0.16, 0.36, 0.64, 1.  ])

add_dimension(dimension)

Add the specified dimension to this patch

Input

• dimension - (Dimension) Dimension to be added

add_gauges(gauge_coords)

Determine the cell indices of each gauge and make a list of all gauges with their cell indices.

c_center(ind)

Compute center of computational cell with index ind.

c_centers_with_ghost(num_ghost)

Calculate the coordinates of the cell centers, including ghost cells, in the computational domain.

Input

• num_ghost - (int) Number of ghost cell layers

c_nodes_with_ghost(num_ghost)

Calculate the coordinates of the cell nodes (corners), including ghost cells, in the computational domain.

Input

• num_ghost - (int) Number of ghost cell layers

get_dim_attribute(attr)

Returns a tuple of all dimensions’ attribute attr

p_center(ind)

Compute center of physical cell with index ind.

plot(num_ghost=0, mapped=True, mark_nodes=False, mark_centers=False)

Make a plot of the grid.

By default the plot uses the mapping grid.mapc2p and does not show any ghost cells. This can be modified via the arguments mapped and num_ghost.

Returns a handle to the plot axis object.

setup_gauge_files(outdir)

Creates and opens file objects for gauges.

property c_centers

(list of ndarray(…)) - List containing the arrays locating the computational locations of cell centers, see _compute_c_centers() for more info.

property c_nodes

(list of ndarray(…)) - List containing the arrays locating the computational locations of cell nodes, see _compute_c_nodes() for more info.

property dimensions

(list) - List of Dimension objects defining the grid’s extent and resolution

gauge_dir_name = None

(string) - Name of the output directory for gauges. If the Controller class is used to run the application, this directory by default will be created under the Controller outdir directory.

gauge_file_names = None

(list) - List of file names to write gauge values to

gauge_files = None

(list) - List of file objects to write gauge values to

gauges = None

(list) - List of gauges’ indices to be filled by add_gauges method.

property num_dim

(int) - Number of dimensions

property p_centers

(list of ndarray(…)) - List containing the arrays locating the physical locations of cell centers, see _compute_p_centers() for more info.

property p_nodes

(list of ndarray(…)) - List containing the arrays locating the physical locations of cell nodes, see _compute_p_nodes() for more info.

pyclaw.geometry.Dimension

class clawpack.pyclaw.geometry.Dimension(lower, upper, num_cells, name='x', on_lower_boundary=None, on_upper_boundary=None, units=None)

Basic class representing a dimension of a Patch object

Initialization

Required arguments, in order:

• lower - (float) Lower extent of dimension

• upper - (float) Upper extent of dimension

• num_cells - (int) Number of cells

Optional (keyword) arguments:

• name - (string) string Name of dimension

• units - (string) Type of units, used for informational purposes only

Output:

• (Dimension) - Initialized Dimension object

Example:

>>> from clawpack.pyclaw.geometry import Dimension
>>> x = Dimension(0.,1.,100,name='x')
>>> print(x)
Dimension x:  (num_cells,delta,[lower,upper]) = (100,0.01,[0.0,1.0])
>>> x.name
'x'
>>> x.num_cells
100
>>> x.delta
0.01
>>> x.nodes[0]
0.0
>>> x.nodes[1]
0.01
>>> x.nodes[-1]
1.0
>>> x.centers[-1]
0.995
>>> len(x.centers)
100
>>> len(x.nodes)
101

centers_with_ghost(num_ghost)

(ndarrary(:)) - Location of all cell center coordinates for this dimension, including centers of ghost cells.

nodes_with_ghost(num_ghost)

(ndarrary(:)) - Location of all edge coordinates for this dimension, including nodes of ghost cells.

property centers

(ndarrary(:)) - Location of all cell center coordinates for this dimension

property delta

(float) - Size of an individual, computational cell

property nodes

(ndarrary(:)) - Location of all cell edge coordinates for this dimension

Parallel Geometry Objects

petclaw.geometry.Domain

class clawpack.petclaw.geometry.Domain(geom)

Bases: clawpack.pyclaw.geometry.Domain

Parallel Domain Class

Parent Class Documentation:

2D Classic (Clawpack) solver.

Solve using the wave propagation algorithms of Randy LeVeque’s Clawpack code (www.clawpack.org).

In addition to the attributes of ClawSolver1D, ClawSolver2D also has the following options:

dimensional_split

If True, use dimensional splitting (Godunov splitting). Dimensional splitting with Strang splitting is not supported at present but could easily be enabled if necessary. If False, use unsplit Clawpack algorithms, possibly including transverse Riemann solves.

transverse_waves

If dimensional_split is True, this option has no effect. If dimensional_split is False, then transverse_waves should be one of the following values:

ClawSolver2D.no_trans: Transverse Riemann solver not used. The stable CFL for this algorithm is 0.5. Not recommended.

ClawSolver2D.trans_inc: Transverse increment waves are computed and propagated.

ClawSolver2D.trans_cor: Transverse increment waves and transverse correction waves are computed and propagated.

Note that only the fortran routines are supported for now in 2D.

Parent Class Documentation:

Generic classic Clawpack solver

All Clawpack solvers inherit from this base class.

mthlim

Limiter(s) to be used. Specified either as one value or a list. If one value, the specified limiter is used for all wave families. If a list, the specified values indicate which limiter to apply to each wave family. Take a look at pyclaw.limiters.tvd for an enumeration. Default = limiters.tvd.minmod

order

Order of the solver, either 1 for first order (i.e., Godunov’s method) or 2 for second order (Lax-Wendroff-LeVeque). Default = 2

source_split

Which source splitting method to use: 1 for first order Godunov splitting and 2 for second order Strang splitting. Default = 1

fwave

Whether to split the flux jump (rather than the jump in Q) into waves; requires that the Riemann solver performs the splitting. Default = False

step_source

Handle for function that evaluates the source term. The required signature for this function is:

def step_source(solver,state,dt)

kernel_language

Specifies whether to use wrapped Fortran routines (‘Fortran’) or pure Python (‘Python’). Default = 'Fortran'.

verbosity

The level of detail of logged messages from the Fortran solver. Default = 0.

petclaw.geometry.Patch

class clawpack.petclaw.geometry.Patch(dimensions)

Bases: clawpack.pyclaw.geometry.Patch

Parallel Patch class.

Parent Class Documentation:

Global Patch information

Each patch has a value for level and patch_index.