Michaelis-Menten Kinetics and Briggs-Haldane Kinetics

The Michaelis-Menten model (1) is the one of the simplest and best-known approaches to enzyme kinetics. It takes the form of an equation relating reaction velocity to substrate concentration for a system where a substrate S binds reversibly to an enzyme E to form an enzyme-substrate complex ES, which then reacts irreversibly to generate a product P and to regenerate the free enzyme E. This system can be represented schematically as follows:

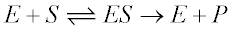
The Michaelis-Menten equation for this system is:

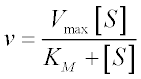
Here, V_max represents the maximum velocity achieved by the system, at maximum (saturating) substrate concentrations. K_M (the Michaelis constant; sometimes represented as K_S instead) is the substrate concentration at which the reaction velocity is 50% of the V_max. [S] is the concentration of the substrate S.

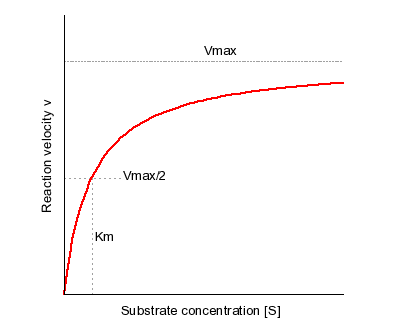
This is a plot of the Michaelis-Menten equation’s predicted reaction velocity as a function of substrate concentration, with the significance of the kinetic parameters V_max and K_M graphically depicted.

The best derivation of the Michaelis-Menten equation was provided by George Briggs and J.B.S. Haldane in 1925 (2), and a version of it follows:

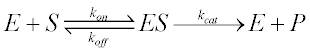
For the scheme previously described, k_on is the bimolecular association rate constant of enzyme-substrate binding; k_off is the unimolecular rate constant of the ES complex dissociating to regenerate free enzyme and substrate; and k_cat is the unimolecular rate constant of the ES complex dissociating to give free enzyme and product P.

Note that k_on has units of concentration^-1time^-1, and k_off and k_cat have units of time^-1. Also, by definition the dissociation binding constant of the ES complex, K_D is given by k_off/k_on (and so has units of concentration).

Once these rate constants have been defined, we can write equations for the rates of change of all the chemical species in the system:

The last of these equations – describing the rate of change of the ES complex – is the most important for our purposes. In most systems, the ES concentration will rapidly approach a steady-state – that is, after an initial burst phase, its concentration will not change appreciably until a significant amount of substrate has been consumed. This steady-state approximation is the first important assumption involved in Briggs and Haldane’s derivation. This is also the reason that well-designed experiments measure reaction velocity only in regimes where product formation is linear with time. As long as we limit ourselves to studying initial reaction velocities, we can assume that [ES] is constant:

In order to determine the rate of product formation (d[P]/dt = k_cat[ES]), we need to rearrange the equation above to calculate [ES]. We know that the free enzyme concentration [E] is equal to the total enzyme concentration [E_T] minus [ES]. Making these substitutions gives us:

We now make a couple of substitutions to arrive at the familiar form of the Michaelis-Menten equation. Since V_max is the reaction velocity at saturating substrate concentration, it is equal to k_cat [ES] when [ES] = [E_T]. We also define K_M in terms of the rate constants as follows:

Note that [S] here represents the free substrate concentration, but typically is assumed to be close to the total substrate concentration present in the system. This second assumption is the free ligand approximation, and is valid as long the total enzyme concentration is well below the K_M of the system. If this condition is not met (for instance, with a very high-affinity substrate), then the quadratic (or ‘Morrison’) equation must be used instead.

Comparing K_M [= (k_off + k_cat)/k_on] and K_D [= k_off/k_on], it is obvious that K_M must always be greater than K_D. Michaelis and Menten assumed that substrate binding and dissociation occurred much more rapidly than product formation (k_cat << k_off, the rapid equilibrium approximation), and that therefore the K_M would be very close to the K_D. The larger the k_cat is relative to k_off, the greater the difference between K_D and K_M. Briggs and Haldane made no assumptions about the relative values of k_off and k_cat, and so Michaelis-Menten kinetics are a special case of Briggs-Haldane kinetics. The opposite extreme, where k_cat >> k_off, is called Van Slyke-Cullen behavior (3).

1. Michaelis, L.,and Menten, M. (1913) Die kinetik der invertinwirkung, Biochemistry Zeitung 49, 333-369.
2. Briggs, G. E., and Haldane, J. B. (1925) A Note on the Kinetics of Enzyme Action, Biochem J 19, 338-339.
3. Van Slyke, D. D., and Cullen, G. E. (1914) The Mode of Action of Urease and of Enzymes in General, J Biol Chem 19, 141-180.

Next: the Quadratic Velocity Equation