I. 2: The Quadratic Velocity Equation for Tight-Binding Substrates
Three assumptions are implicit in Michaelis-Menten kinetics: the steady-state approximation, the free ligand approximation and the rapid equilibrium approximation. (The Briggs-Haldane approach frees us from the last of these three.)

Now consider the second assumption in the list: the free ligand approximation. Remember that this approximation states that the free substrate concentration (the [S] in the Michaelis-Menten equation) is close to the total substrate concentration in the system – which is, in fact, the true independent variable in most experimental set-ups. After all, we know how much substrate we’ve added to reaction mixture, but we don’t know a priori how much of that substrate remains free in solution at steady-state. The free ligand approximation does not hold when a substrate’s KM is lower than the total enzyme concentration, because at low substrate concentrations, a significant fraction of substrate will be bound to the enzyme.
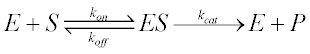
For such unusual cases, we derive a kinetic equation from the scheme above without resorting to the free ligand approximation. The rates of change of the various species are given by four differential equations:
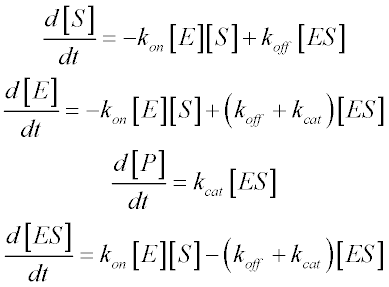
We can assume that ES levels achieve steady-state:
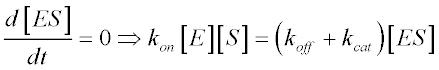
Given that free enzyme concentration [E] equals total enzyme concentration [ET] minus [ES] and that [S] equals total enzyme concentration, we have:
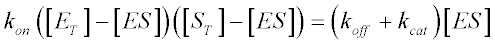
A little algebra gives us:

This is a quadratic equation of
the form a2x + bx + c = 0, whose roots are
given by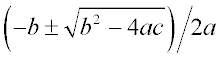 .
.
Making the following substitutions and choosing the relevant (saturable) root gives us:

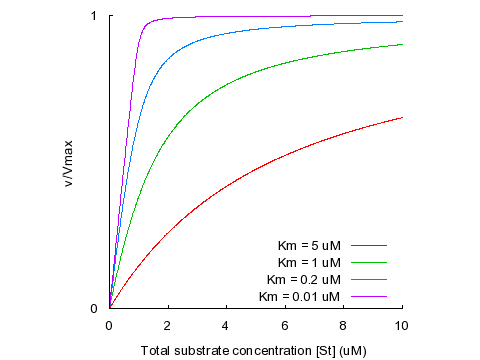
This is the quadratic velocity equation, sometimes also called the tight-binding equation or the Morrison equation (1). As the KM becomes larger than [ET], the curve described by the quadratic equation approaches the hyperbola described by the Michaelis-Menten equation. As the KM becomes lower, the inflection point of the curve (located where [ST] = [ET]) becomes progressively sharper. This is illustrated in the plot below, where the KM varies from 5 times the total enzyme concentration ([ET] = 1 μM) to one-hundredth of [ET]. Differences in affinity between very tight-binding substrates are reflected in the sharpness of the inflection, meaning that KM values recovered from fits to experimental data are disproportionately sensitive to error in the data points surrounding the inflection point. As a rule of thumb, the quadratic equation should be used in preference to the Michaelis-Menten equation whenever the KM is less than five-fold larger than [ET].
Derivations of this type that do not use the free ligand approximation grow rapidly more complicated for more complex kinetic systems. For anything more complicated than a one-site model, it is better to use kinetic simulations as detailed in part II of this guide.
- Morrison, J. F. (1969) Kinetics of the reversible inhibition of enzyme-catalysed reactions by tight-binding inhibitors, Biochimica et Biophysica Acta (BBA) - Enzymology 185, 269-286.