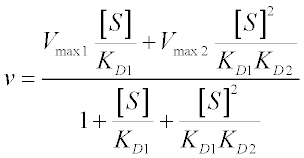I.3: Multiple Binding: Sequential Models
Building on the derivation of Michaelis-Menten kinetics, we now turn to enzymes with multiple substrate-binding sites.
Early work in this regard was carried out by Adair and Pauling, operating under the rapid equilibrium approximation. Remember that this assumption states that all substrate binding and dissociation steps happen much more rapidly than catalytically productive steps. In 1954, King and Altman showed how to solve any kinetic system without resorting to this approximation, but this is unnecessarily complicated for our purposes. Even if the rapid equilibrium approximation does not hold for our system, the forms of the equations we derive will not change – instead, the significance of the various KM values will be different. This is analogous to the difference between KM (or KD) in the Michaelis-Menten model and KM in the Briggs-Haldane model.
We begin with the simplest model of multiple binding: a two-site sequential model. Here, an enzyme E can bind a single molecule of substrate S to form a singly-occupied complex ES with equilibrium dissociation constant KD1. ES can either react irreversibly to form product P with rate kcat1, or can bind a second substrate molecule S to form a doubly-occupied complex ESS with dissociation constant KD2. In turn, ESS can irreversibly form P with rate kcat2. This is represented schematically below:

In order to calculate the reaction velocity for this system, we need to know the relative concentrations of the active species ES and ESS. We will describe a straightforward derivation of these quantities, and then a shortcut that allows one to quickly solve more complicated kinetic systems.
From the definitions of the two dissociation constants, we have:

Relative to the total enzyme concentration, ET:
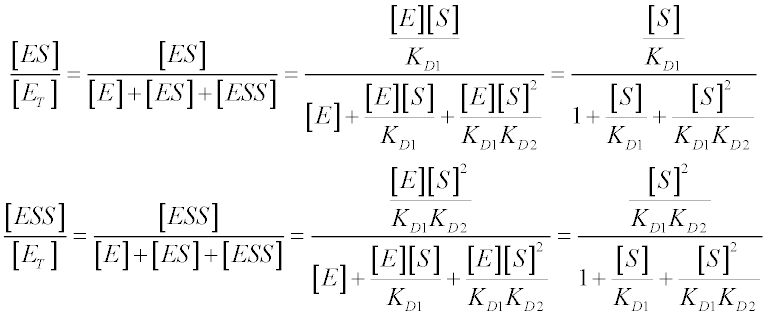
The total reaction velocity for this system is given by (where Vmax1 = kcat1[ET] and Vmax2 = kcat2[ET]):
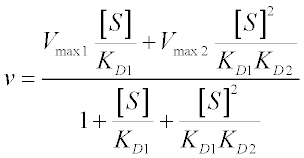
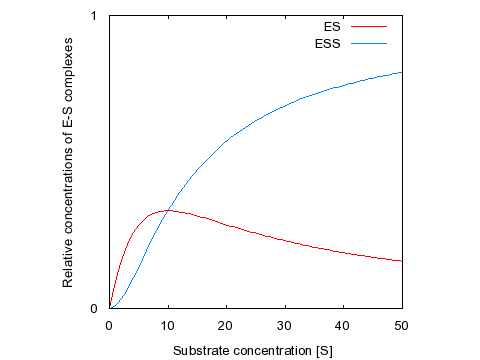
This graph shows the relative concentrations of the two active species as a function of substrate concentration, when both KDs are set to 10 μM. Note the initial increase and subsequent decrease in the level of ES, while the concentration curve for ESS is sigmoidal. Therefore, if Vmax1 (for ES) is much greater than Vmax2 (for ESS) then the system will exhibit substrate inhibition kinetics; if Vmax2 is much greater than Vmax1 then the system will exhibit sigmoidal kinetics. We will return to this idea when we discuss allosterism in more detail.
There is a quicker way to calculate reaction velocity equations of this type. To return to the scheme of a two-site sequential model:

Each species in the system has a relative concentration term that appears in the denominator of the velocity equation, while terms from all active species appear in the numerator. To find the relative concentration term of any species, simply work your way backwards from that species to the free enzyme; the specific term is equal to the product of all the substrate molecules that bind, divided by all the equilibrium constants in the chain. So the specific term for ES is [S]/KD1 and the term for ESS is [S]2/KD1KD2. The specific term for free enzyme is always 1.
The denominator of the velocity equation is the sum of all specific terms: 1 + [S]/KD1 + [S]2/KD1KD2; the numerator is the sum of specific terms for catalytically active species, each weighted by their respective Vmax values – and voila: